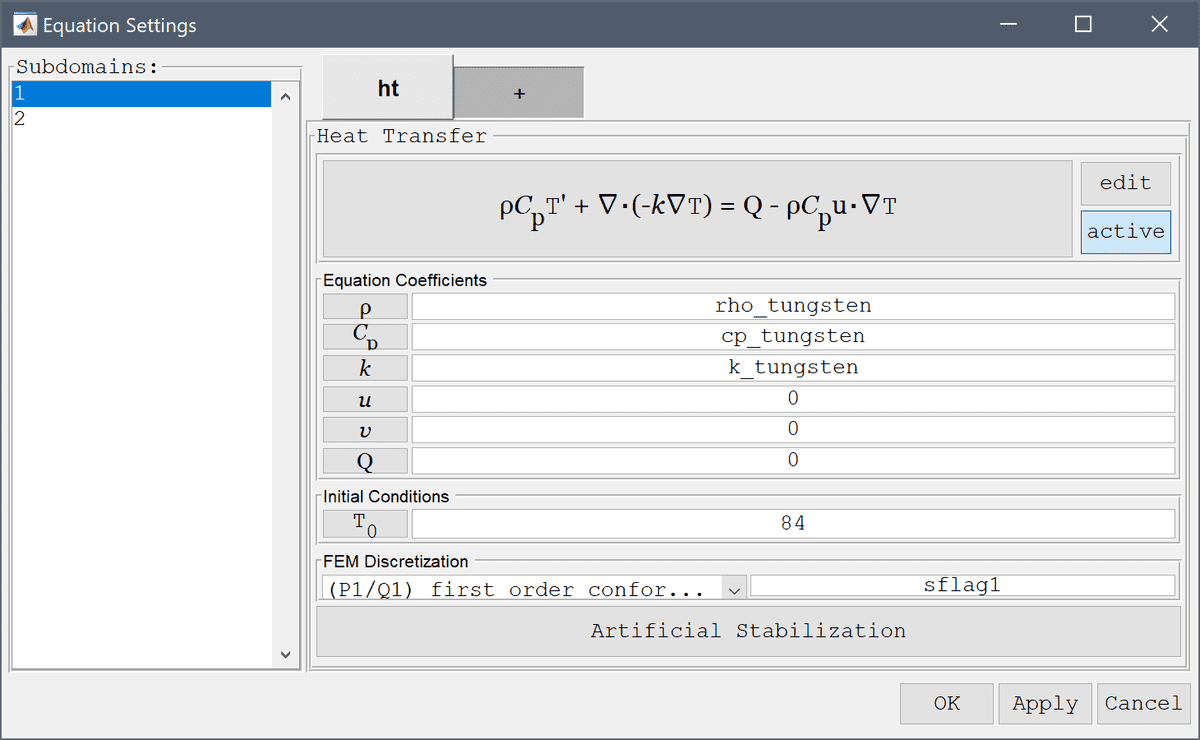
FEATool supports modeling heat transfer through both conduction, that is heat transported by a diffusion process, and convection or advection, which is heat transported through a fluid through convection by a velocity field. The heat transfer physics mode supports both these processes, and is defined by the following equation
\[ \rho C_p\frac{\partial T}{\partial t} + \nabla\cdot(-k\nabla T) = Q - \rho C_p\mathbf{u}\cdot\nabla T \]
where ρ is the density, Cp the heat capacity, k is the thermal conductivity, Q heat source term, and u a vector valued convective velocity field. In the Equation Settings dialog box show below the equation coefficients, initial value for the temperature T, and finite element shape function space can be specified (note that here the convective velocities u and v are the dependent variables from a coupled incompressible fluid flow physics mode, but can also be constants and complex expressions).
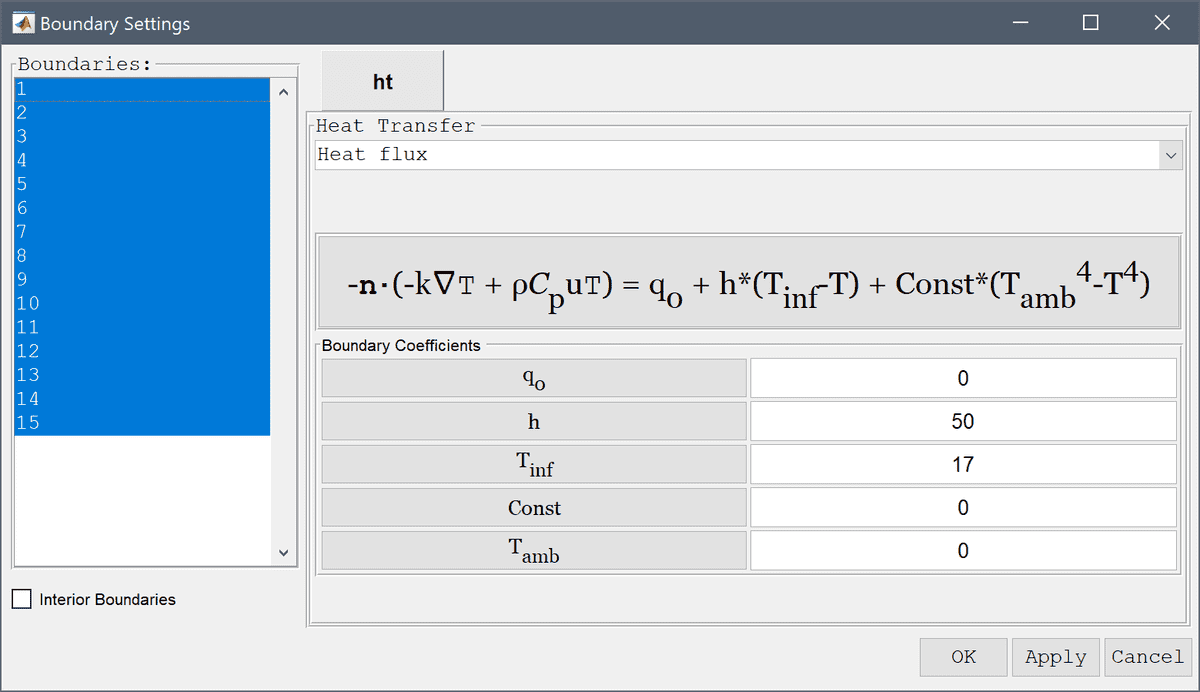
The heat transfer physics mode allows for four different boundary conditions types.
- Temperature, T0 Prescribes the temperature on the boundary to T0.
Note that T0 does not have to be a constant either but as all coefficients in FEATool can be complex expression involving space coordinates, dependent variables, and derivatives.
- Convective flux, -n·k∇T = 0
This boundary condition prescribes a zero diffusive flux leaving the convective flux unspecified and free which is appropriate for outflow boundaries in fluids.
- Thermal insulation/symmetry, -n·(k∇T + ρCpuT) = 0
This condition sets the heat flux at the boundary to zero which is appropriate for insulated and symmetry boundaries.
- Heat flux, -n·(k∇T + ρCpuT) = q0
The heat flux boundary condition allows the heat flux q0
at the boundary to be prescribed. As with the temperature condition,
q0 allows for complex expressions such as the common
convective and radiation conditions to a surrounding medium, in this
cases one could for example set q0 = h*(T_amb-T) +
c_rad*(T_amb-T)^4 where T_amb is the ambient temperature of the
surrounding fluid, and c_rad a constant for the radiation term. T
is the name of dependent variable from the physics mode and h is the
heat transfer coefficient between the boundaries and surrounding
medium.
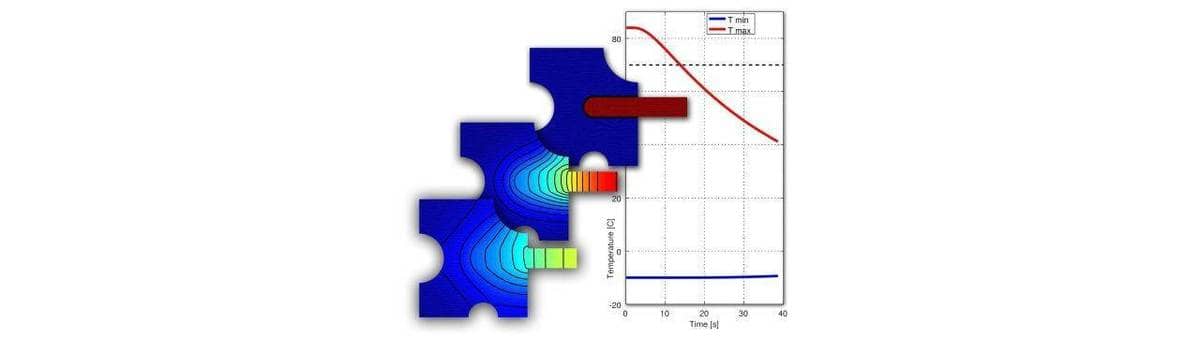
A model example that incorporates these heat transfer effects is a
transient cooling for shrink fitting a two part assembly [1]. A
tungsten rod heated to 84 °C is inserted into a -10 °C chilled
steel frame part. The time when the maximum temperature has cooled to
70 °C should be determined. The assembly is cooled due to convection
through a surrounding medium kept at 17 °C and a heat transfer
coefficient of 50 W/(m2 K) thus heat flux boundary
conditions are prescribed on all boundaries as q0 =
h*(17-T).
The FEATool tutorial for the model can be viewed in the tutorial section of the User’s Guide
References
[1] Krysl P. A Pragmatic Introduction to the Finite Element Method for Thermal and Stress Analysis. Pressure Cooker Press, USA, 2005.