Multi-Simulation and External Solvers in FEATool
With the external solver and multi-simulation interfaces, FEATool Multiphysics makes it easy to use multiple solvers which can be suitable for different classes of problems. Using more than one solver can also be very helpful in validating physics models and simulations, as one can compare results directly for several solution methods.
With FEATool, direct knowledge about how the external solvers actually work is not required, as model and mesh conversion and export, solver control, solution interpolation and re-import are all handled conveniently and automatically by the external solver interface. This saves a significant amount of time as models only need to be set up and defined once with the easy FEATool GUI or MATLAB CFD and CLI interface (instead of once for each solver).
In the following, the built-in FEATool multiphysics solver, dedicated OpenFOAM computational fluid dynamics (CFD) solver, and general FEniCS finite element analysis (FEA) solver will be compared for the same benchmark test case.
Flow Around Cylinder Benchmark Test Case
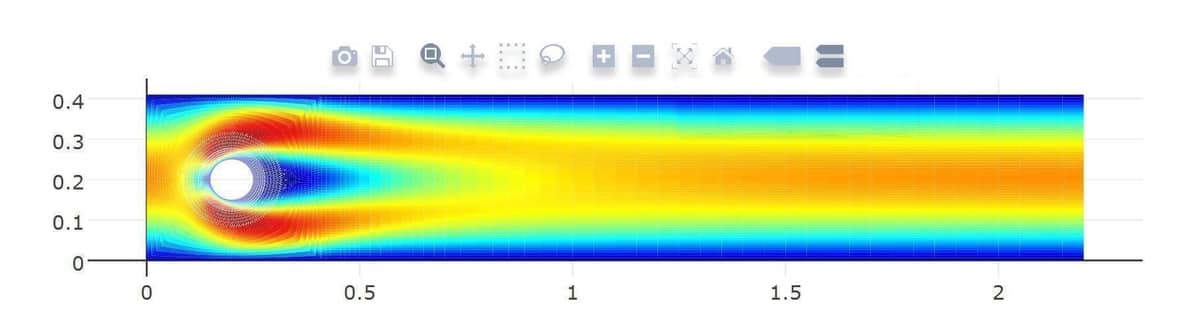
A classic laminar and incompressible flow around cylinder CFD test case is used to evaluate the efficiency of the solution methods [1]. Very accurate reference solutions for drag, lift, and pressure difference have been established for this benchmark [2]. The test case is described in more detail in the flow around a cylinder tutorial example which can found in the FEATool User’s Guide. A video tutorial is also available showing step by step how to set up the model in the FEATool GUI
Although the benchmark simulations can be performed just as well in the GUI, it is usually more convenient to write a MATLAB m-script file, which then can be run automatically (and repeated for reproducibility). FEATool m-script model files can either be written completely from scratch, or conveniently exported from the GUI using the Save As M-Script Model… option in the File menu (this will translate each GUI action to a corresponding MATLAB function call and export it to an editable plain text file).
The computational grid employed in this study is the same structured quadrilateral mesh used in reference [2]. The cylinder flow benchmark grid is constructed using the structured grid primitives and joined together. Up to four successive uniform refinements (five grid levels) are used to observe the convergence behavior with respect to the mesh size. The table below shows the grid statistics as well as the total number of unknowns (degrees of freedom) for the solvers.
| Grid Level | ngrid cells | ngrid points | nunknowns | ||
|---|---|---|---|---|---|
| FEATool | OpenFOAM | FEniCS | |||
| 1 | 416 | 246 | 2440 | 624 | 2062 |
| 2 | 1664 | 908 | 9456 | 2496 | 7868 |
| 3 | 6656 | 3480 | 37216 | 9984 | 30712 |
| 4 | 26624 | 13616 | 147648 | 39936 | 121328 |
| 5 | 106496 | 53856 | 588160 | 159744 | 482272 |
FEATool Multiphysics Solver
FEATool features dedicated solvers for both stationary and time dependent coupled multiphysics problems. PDEs are are discretized with the finite element method (FEM) as a single fully coupled system. This approach means that all equations and unknowns are solved together in one step. In contrast to traditional splitting and segregated solution approaches where equations are decoupled and solved sequentially, a fully coupled (monolithic) solver typically features better convergence and robustness, at the cost of system size and increased memory requirements. The ensuing sparse linear systems are in turn solved with the direct solver built into MATLAB, which currently defaults to SuiteSparse’s UMFPACK.
In the present benchmark the Navier-Stokes equations are discretized
with the Q2P-1 finite element shape function
space for quadrilateral cells (second order velocity and first order
discontinuous pressure approximation). To call the FEATool stationary
solver the solvestat function is used
fea.sol.u = solvestat( fea, 'jac', jac );
where fea is a FEATool finite element data struct, and
jac a user defined analytic Newton Jacobian (which is
faster than using a numerical Jacobian). Fixed-point Picard iterations
will be used for non-linear problems if the jac argument is omitted. The
resulting solution vector is stored in the fea.sol.u
field.
The resulting drag cD, and lift cL coefficients, and pressure difference between front and rear of the cylinder, Δp, can be seen in the table below. The required CPU time in seconds is denoted by tsolve and the number of non-linear iterations it. As can be seen the solutions converge nicely towards the reference values as the mesh density increases.
| Grid Level | tsolve | it | cD | cL | Δp |
|---|---|---|---|---|---|
| 1 | 3.7 | 6 | 5.54487950165 | 0.008442514119 | 0.11786516773 |
| 2 | 4.1 | 6 | 5.57184497660 | 0.010597174013 | 0.11750789738 |
| 3 | 11.3 | 6 | 5.57822330883 | 0.010616116637 | 0.11750614625 |
| 4 | 47.1 | 6 | 5.57930237757 | 0.010617056264 | 0.11751529098 |
| 5 | 376.1 | 6 | 5.57949098460 | 0.010618321893 | 0.11751879230 |
| Ref.[1],[2] | 5.57953523384 | 0.010618937712 | 0.11752016697 |
OpenFOAM CFD Solver
OpenFOAM is the leading leading free, open source software for computational fluid dynamics (CFD) [3]. Featuring dedicated solvers and support for many types of flow regimes such as incompressible and compressible, turbulent, non-isothermal, and multiphase flows, OpenFOAM is a very versatile flow solver package. To discretize the equations OpenFOAM uses a cell centered finite volume method (FVM), with operator splitting and iterative linear solvers. For steady state calculations, such as featured in this benchmark test case, the Simple scheme is employed with pseudo time stepping.
OpenFOAM is a quite complicated and complex software code, designed
for the command line, and usually takes significant time and effort to
learn how to use properly. To make this easier, FEATool includes
dedicated functionality automate solving fluid mechanics problems with
a GUI for OpenFOAM. Instead of using the solvestat function to call the FEATool
solver as above, one can instead use the openfoam
function call
fea = openfoam( fea );
This automatically converts incompressible Navier-Stokes flow problems to OpenFOAM case files (including extruding 2D meshes to 3D), solves them with OpenFOAM, and imports the resulting solutions back into FEATool. (Note that the actual OpenFOAM and external solver binaries have to be installed separately, as they are not included with the FEATool distribution.)
The resulting benchmark quantities are presented in the table below (here it designates the number of pseudo time steps required to reach steady state). The results produced by OpenFOAM are not as accurate as for the FEATool solver. This can possibly be attributed to the cell centered constant discretization which can not yield the same accuracy as a higher order one.
| Grid Level | tsolve | it | cD | cL | Δp |
|---|---|---|---|---|---|
| 1 | 4.0 | 66 | 5.15961787318 | 0.016487323804 | 0.09551670000 |
| 2 | 6.2 | 79 | 5.35193993474 | 0.010635832139 | 0.11048305000 |
| 3 | 28.9 | 189 | 5.53487563438 | 0.012056572542 | 0.11553345000 |
| 4 | 255.5 | 585 | 5.59739806743 | 0.012364196670 | 0.11737575000 |
| 5 | 3053.0 | 1900 | 5.61958135978 | 0.012736477867 | 0.11810605000 |
| Ref.[1],[2] | 5.57953523384 | 0.010618937712 | 0.11752016697 |
FEniCS FEA Solver
FEniCS is designed to quickly translate scientific models into efficient finite element code and be a computing platform for solving partial differential equations (PDEs). The FEniCS Project finite element analysis (FEA) solver is, similar to FEATool Multiphysics, designed to be able to solve general systems of coupled equations.
FEniCS features its own PDE syntax and language to which FEATool
models can be directly converted and exported. This can be
accomplished with help of the fenics interface FEATool function as
fenics( fea, 'mode', 'export' );
fenics( fea, 'mode', 'solve' );
fea = fenics( fea, 'mode', 'import' );
where the mode argument specifies which solver phase or
action to take. (This will in a future release be simplified to a
single call as for the other solvers.)
In contrast to FEATool, FEniCS currently only supports simplex mesh cell shapes (triangles in 2D and tetrahedra in 3D). The structured benchmark grid is therefore subdivided into triangles for the FEniCS simulations. As for FEM shape functions FEniCS here employs the P2P1 Taylor-Hood mixed finite element space for the Navier-Stokes equations. As for sparse linear solver the default (direct PETSc) solver is used.
From the results shown in the table below it can be seen that convergence results similar to those for FEATool is achieved. This is also expected as FEniCS per default also employs a fully coupled monolithic approach (although operator splitting is supported but has to be implemented manually). As the FEniCS results are interpolated to the grid points before re-import into MATLAB and FEATool, some accuracy in the velocity space is also expected to have been lost. (In critical applications FEniCS post-processing might better be performed in FEniCS/Python as it is not quite clear how to export higher order unknowns, or how the degrees of freedom are internally reordered.)
| Grid Level | tsolve | it | cD | cL | Δp |
|---|---|---|---|---|---|
| 1 | 0.2 | 5 | 5.34109374154 | 0.010757363546 | 0.11735706956 |
| 2 | 0.9 | 5 | 5.49233845223 | 0.014695899352 | 0.11747082573 |
| 3 | 4.1 | 5 | 5.54117954222 | 0.011828289208 | 0.11749692232 |
| 4 | 26.4 | 5 | 5.56158878050 | 0.011065243466 | 0.11751324363 |
| 5 | 202.0 | 5 | 5.57073050210 | 0.010815860398 | 0.11751801083 |
| Ref.[1],[2] | 5.57953523384 | 0.010618937712 | 0.11752016697 |
Solver Comparison
The resulting CPU timings as a function of accuracy (cost vs. accuracy) are shown in the figures below. With respect to drag and lift coefficients the FEATool Multiphysics solver performs significantly better than both OpenFOAM and FEniCS (although technically FEniCS should eventually be able to achieve the same accuracy). For the pressure drop measure, FEniCS and FEATool was roughly equal while the OpenFOAM results were about two orders less accurate for the same computational cost. As for convergence FEATool featured better convergence for the drag coefficient, while lift and pressure was linear as for FEniCS. OpenFOAM seemed in particular to have issues with the finest grid, as well as the lift coefficient (which is the most difficult quantity to compute accurately).
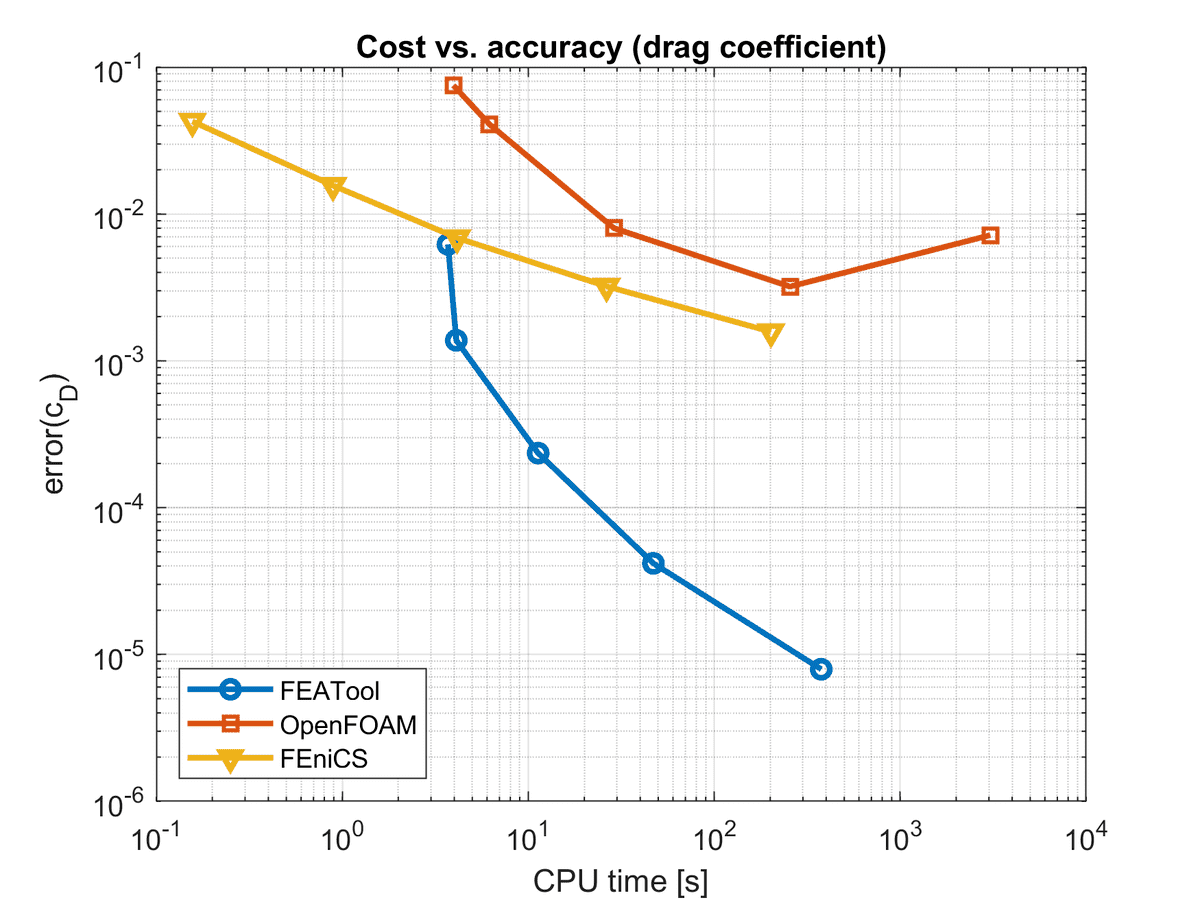
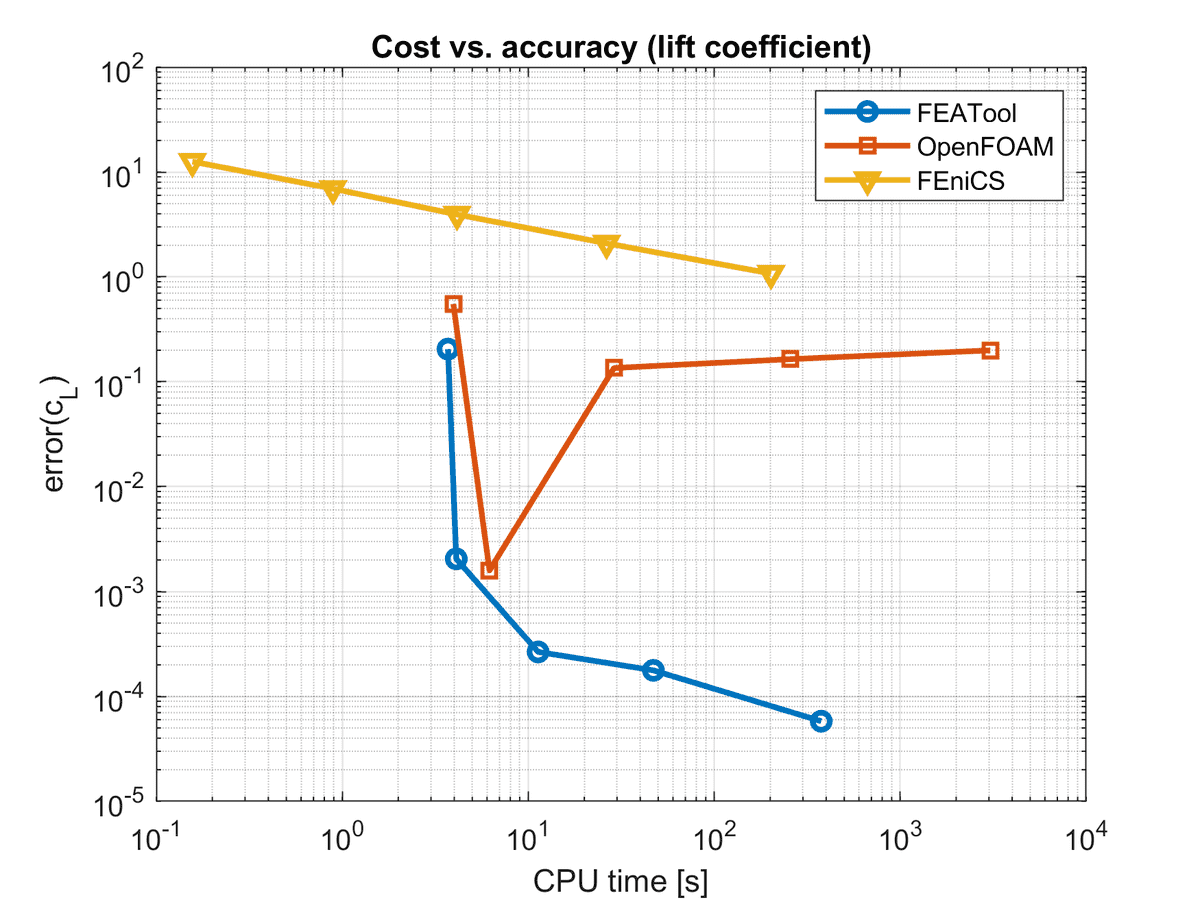
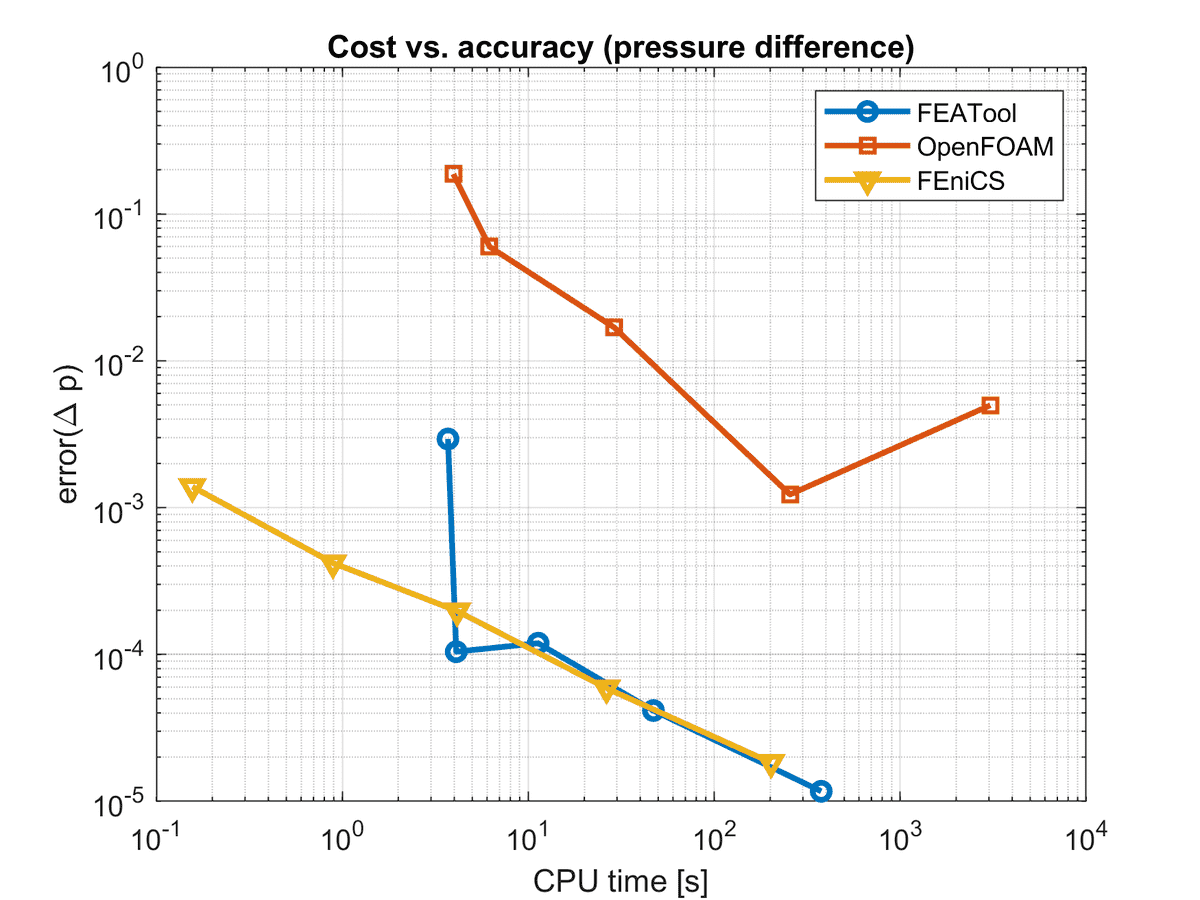
To summarize one can say that for this steady laminar flow test case (Re = 20) fully coupled monolithic solvers, such as used in FEATool and FEniCS, seem to be the best choice. Here OpenFOAM computed overall less accurate and uncertain results for a given CPU effort. In particular OpenFOAM showed weak scaling with respect to mesh density (increasing number of iterations to converge). The benefit of OpenFOAM it that due to the splitting approach and iterative solvers, less memory is required and larger mesh sizes can be used. In the future it might be interesting to extend the study to instationary test cases which might more be in favor of OpenFOAM and operator splitting (which can be implemented as custom solver approaches in both FEATool and FEniCS).
CFD Benchmark Download
The CFD benchmarking script used here has been written as a convenient and self contained FEATool MATLAB m-script file and can be downloaded from the link below
References
[1] G. Nabh, On higher order methods for the stationary incompressible Navier-Stokes equations, PhD Thesis, 1998, University of Heidelberg. Preprint 42 / 98, 1998.
[2] V. John, G. Matthies, Higher-order finite element discretizations in a benchmark problem for incompressible flows, International Journal for Numerical Methods in Fluids, 2001, 37:8:885-903.
[3] The OpenFOAM homepage, The OpenFOAM Foundation, London, United Kingdom, 2018.