Having implemented and fully integrated a uniform MATLAB mesh generation framework with FEATool Multiphysics, it is now both very easy and convenient to directly compare mesh generation codes and algorithms with each other. In the following post the DistMesh, Gmsh, and Triangle open source mesh generators are compared for a number of basic mesh generation benchmark test cases (evaluating both grid generation time and mesh quality).
2D Circle Mesh Generation Test
The first test case examines the basic mesh generation on a unit circle. With the FEATool MATLAB CLI and scripting interface the geometry can quickly be created using the circle geometry object primitive as
geom.objects = { gobj_circle() };
In addition to the three external mesh generators, a fourth reference
method using the circgrid
quadrilateral grid primitive (and converting to triangles with
quad2tri) is used
grid1 = quad2tri( circgrid() );
The three other grids are generated with
grid2 = gridgen( geom, 'hmax', hmax, 'gridgen', 'distgrid' ); % DistMesh grid generation call.
grid3 = gridgen( geom, 'hmax', hmax, 'gridgen', 'gmsh' );
grid4 = gridgen( geom, 'hmax', hmax, 'gridgen', 'triangle' );
where hmax specifies the target mesh size. The mesh generation
options are in the following tests left to their defaults, minimum
triangle angle target of 28 degrees for Triangle, and using the
automatic (delaunay) Gmsh algorithm. Furthermore, the generated
grids can be visualized with the
plotgrid command as
plotgrid( grid1 )
The resulting grids with a uniform hmax = 0.2 from the four grid generation methods can be seen in the figure below. DistMesh clearly produces the most uniform result, while the output from Gmsh and Triangle are mixed, and circgrid could be improved locally with triangle splitting testing for quality (tri2quad always splits triangles along the first quadrilateral diagonal).

The timings or CPU time required for mesh generation with hmax = 0.4, 0.2, 0.1, 0.05, 0.025, 0.0125, and 0.00625 (resulting in meshes with a total number of grid cells ranging from 50 to 250,000) can be seen in the next figure. It is clear that the DistMesh (MATLAB m-code) algorithm is the most costly, while Gmsh (C++ code) falls in the middle, and Triangle (C code) and circgrid both are very fast. In the case of DistMesh the Delaunay re-triangulation library calls required about 15% of the total time, so most of the time was spent in the MATLAB code itself (on the finest grid a total of 19 re-triangulations was required and about ~700 iterations for convergence to be achieved).
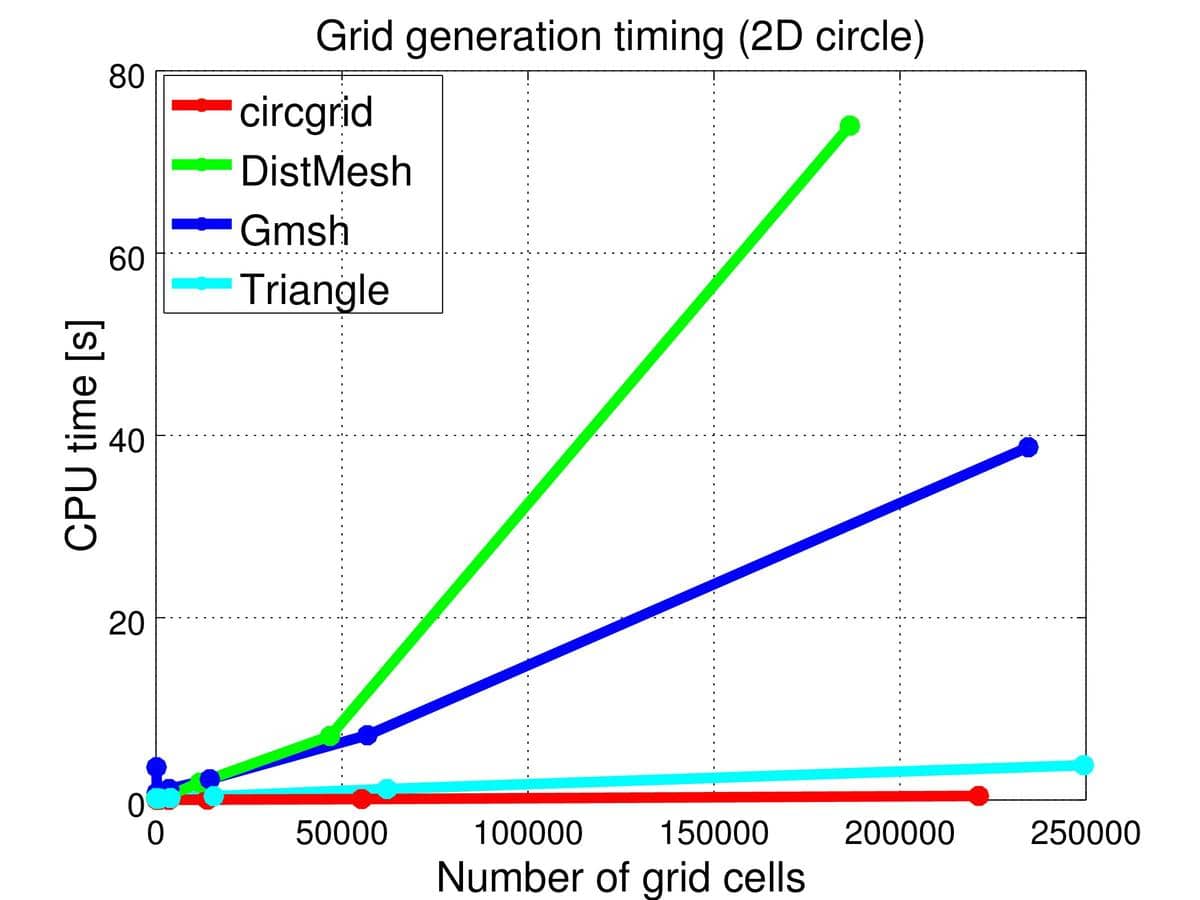
The computed minimum and mean mesh quality measures (here defined as ratio of circumscribed to inscribed bounding circle radius) for the various grid refinement levels can be seen in the tables below. Firstly, for circgrid, as noted above, the minimum mesh quality could likely be improved with a better splitting selection method. Moreover, the minimum mesh quality decreases for both Gmsh and Triangle with increasing mesh the densities, and Gmsh produces (keeps) a few strikingly poor triangles finest meshes. As for the mean mesh quality DistMesh produces close to perfect equilateral triangles with Triangle close behind.
Minimum mesh quality (circle)
L1 L2 L3 L4 L5 L6 L7
---------------------------------------------------------
circgrid | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28 | 0.28
DistMesh | 0.87 | 0.84 | 0.84 | 0.72 | 0.79 | 0.79 | 0.84
Gmsh | 0.49 | 0.47 | 0.42 | 0.42 | 0.25 | 0.02 | 0.01
Triangle | 0.85 | 0.73 | 0.58 | 0.64 | 0.55 | 0.54 | 0.44
---------------------------------------------------------
Mean mesh quality (circle)
L1 L2 L3 L4 L5 L6 L7
---------------------------------------------------------
circgrid | 0.75 | 0.80 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81
DistMesh | 0.97 | 0.98 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00
Gmsh | 0.87 | 0.88 | 0.90 | 0.90 | 0.86 | 0.86 | 0.84
Triangle | 0.95 | 0.95 | 0.96 | 0.95 | 0.95 | 0.95 | 0.96
---------------------------------------------------------
2D Composite Geometry Mesh Generation Test
This second more slightly complex test case involves both a circular hole and inner boundaries (embedded subdomain) in the outer unit square geometry. With the FEATool MATLAB functions this geometry can be defined as
geom.objects = { gobj_rectangle(), ...
gobj_circle( [0.4, 0.4], 0.2, 'C1' ), ...
gobj_circle( [0.75, 0.75], 0.15, 'C2' ) };
geom = geom_apply_formula( geom, 'R1-C1' );
The resulting grids with hmax = 0.1 can be seen in the following figure.
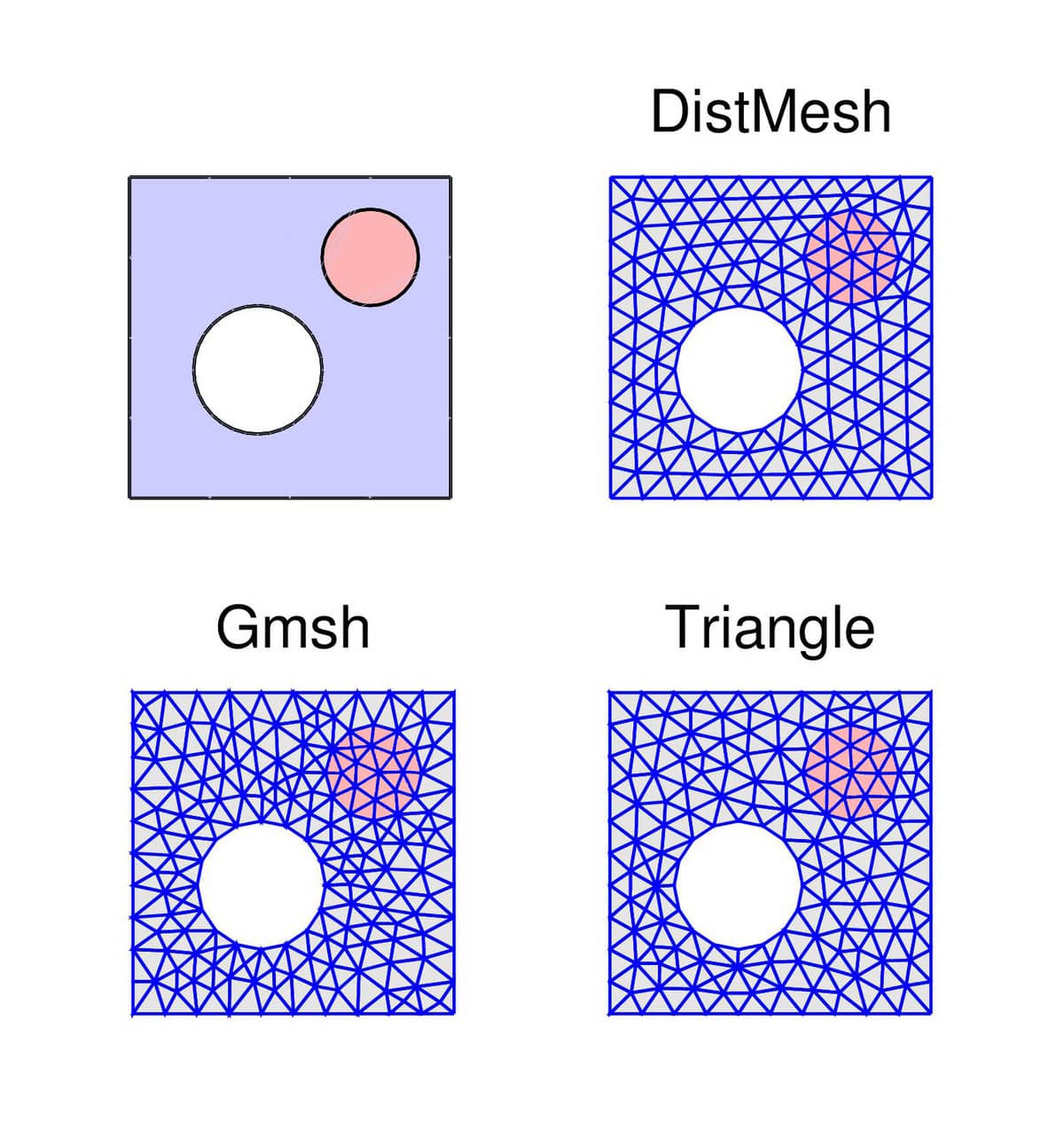
From the grid generation timings in the table below it is clear that Triangle is significantly more efficient than the other approaches. Surprisingly, here Gmsh is actually slower than DistMesh (possibly due to the internal boundaries).
CPU time [s] (composite geometry)
L1 L2 L3 L4 L5 L6
--------------------------------------------------
DistMesh | 0.5 | 1.6 | 1.0 | 1.9 | 2.9 | 13.9
Gmsh | 4.4 | 3.2 | 3.2 | 3.1 | 7.8 | 33.4
Triangle | 0.3 | 0.1 | 0.2 | 0.2 | 0.4 | 1.2
--------------------------------------------------
As for mesh quality DistMesh does also here produce the most uniform meshes while Gmsh allows a few poor quality triangles on the finer grids.
Minimum mesh quality (composite geometry)
L1 L2 L3 L4 L5 L6
--------------------------------------------------
DistMesh | 0.28 | 0.72 | 0.77 | 0.74 | 0.77 | 0.77
Gmsh | 0.55 | 0.59 | 0.53 | 0.35 | 0.29 | 0.26
Triangle | 0.55 | 0.63 | 0.45 | 0.54 | 0.58 | 0.50
--------------------------------------------------
Mean mesh quality (composite geometry)
L1 L2 L3 L4 L5 L6
--------------------------------------------------
DistMesh | 0.91 | 0.96 | 0.98 | 0.99 | 1.00 | 1.00
Gmsh | 0.91 | 0.91 | 0.90 | 0.91 | 0.91 | 0.90
Triangle | 0.91 | 0.92 | 0.94 | 0.95 | 0.95 | 0.95
--------------------------------------------------
3D Cylinder Mesh Generation Test
Finally, a simple 3D mesh generation test case of a single cylinder, defined as
geom.objects = { gobj_cylinder() };
The generated meshes with hmax = 0.2 can be seen in the following figure. Note that Triangle is not included since it only supports 2D mesh generation. Also similar to circgrid in 2D, the cylgrid and hex2tet grid primitives could technically also be used here as a reference.
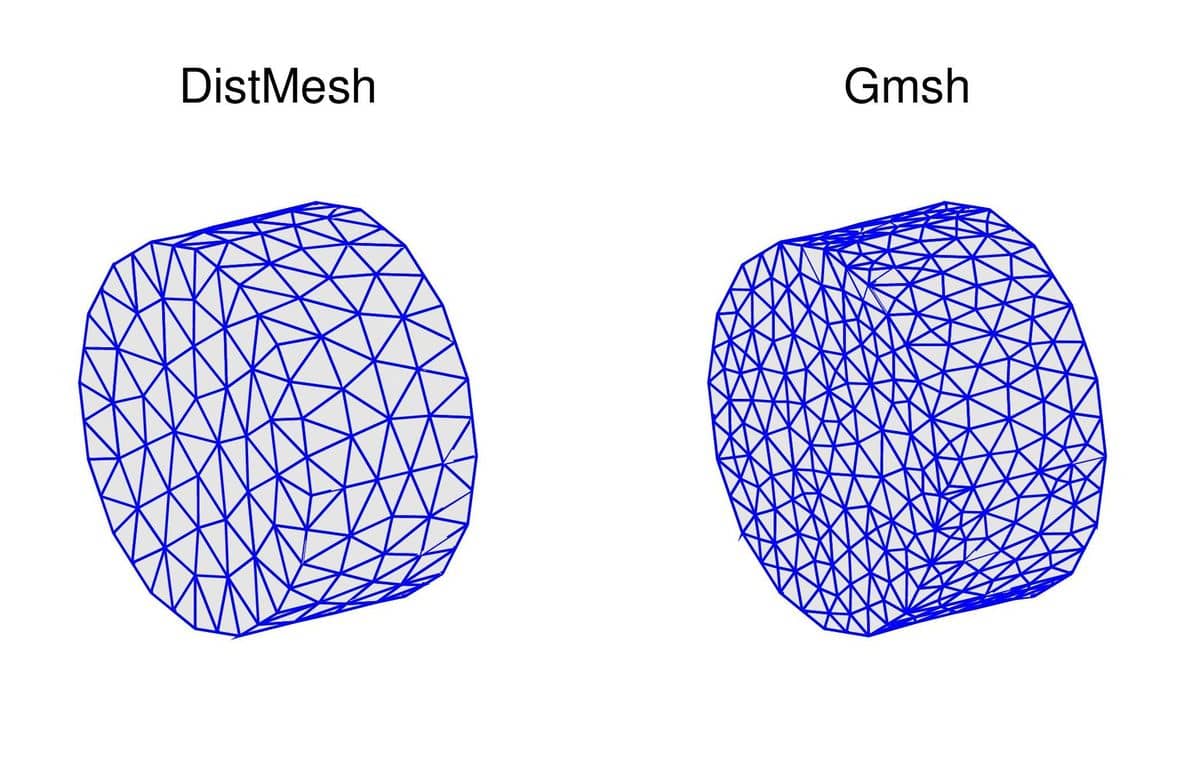
The 3D mesh generation timings are shown below and it is clear that Gmsh is significantly faster than DistMesh (which failed for the finest grid).
CPU time [s] (cylinder)
L1 L2 L3
------------------------------
DistMesh | 4.7 | 45.4 | -
Gmsh | 4.0 | 4.8 | 11.2
------------------------------
With respect to the mesh quality DistMesh produced the best grids although both methods produced a number of poor quality tetrahedra.
Mean mesh quality (cylinder)
L1 L2 L3
------------------------------
DistMesh | 0.9 | 0.9 | -
Gmsh | 0.7 | 0.8 | 0.8
------------------------------
Conclusions
To summarize these mesh generation tests, if a very mesh high quality is required then the DistMesh algorithm is recommended. Otherwise, if quality is not a major factor the Triangle mesh generator is recommended in 2D due to its speed and also robustness. In 3D there are not as many options, but Gmsh seems to do fine in 3D. In 2D Gmsh mesh quality could probably be improved with different settings. However, it is still unlikely it would beat Triangle in speed and can thus not currently be recommended in two dimensions except for using the automatic quadrilateral grid generation functionality (not explored or evaluated here). These recommendations also coincide with the default grid generation settings in the FEATool Multiphysics GUI.