The classic Poisson equation is one of the most fundamental partial differential equations (PDEs). Although one of the simplest equations, it is a very good model for the process of diffusion and comes up in many applications (for example fluid flow, heat transfer, and chemical transport). It is therefore fundamental to many simulation codes to be able to solve it efficiently and accurately.
This example shows how to up and solve the Poisson equation
$$ d_{ts}\frac{\partial u}{\partial t} + \nabla\cdot(-D\nabla u) = f $$
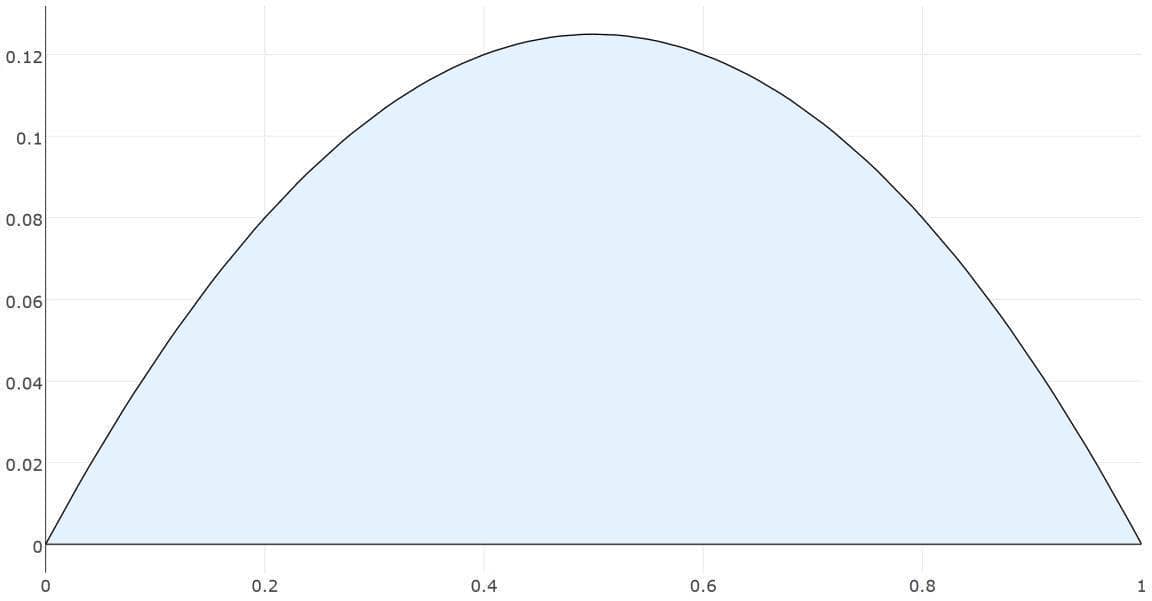
for a scalar field u = u(x) on a unit line. Both the diffusion coefficient D and right hand side source term f are assumed constant and equal to 1. Homogeneous Dirichlet boundary conditions, u = 0 are prescribed on all boundaries of the domain. The Poisson problem is also considered stationary meaning that the time dependent term can be neglected. The exact solution for this problem is u(x) = (-x2+x)/2, which can be used to measure the accuracy of the computed solution.
This model is available as an automated tutorial by selecting Model Examples and Tutorials… > Classic PDE > Poisson Equation from the File menu, and also as the MATLAB simulation m-script example ex_poisson1. Step-by-step and video tutorial instructions, showing how to set up and run this model, are linked below.