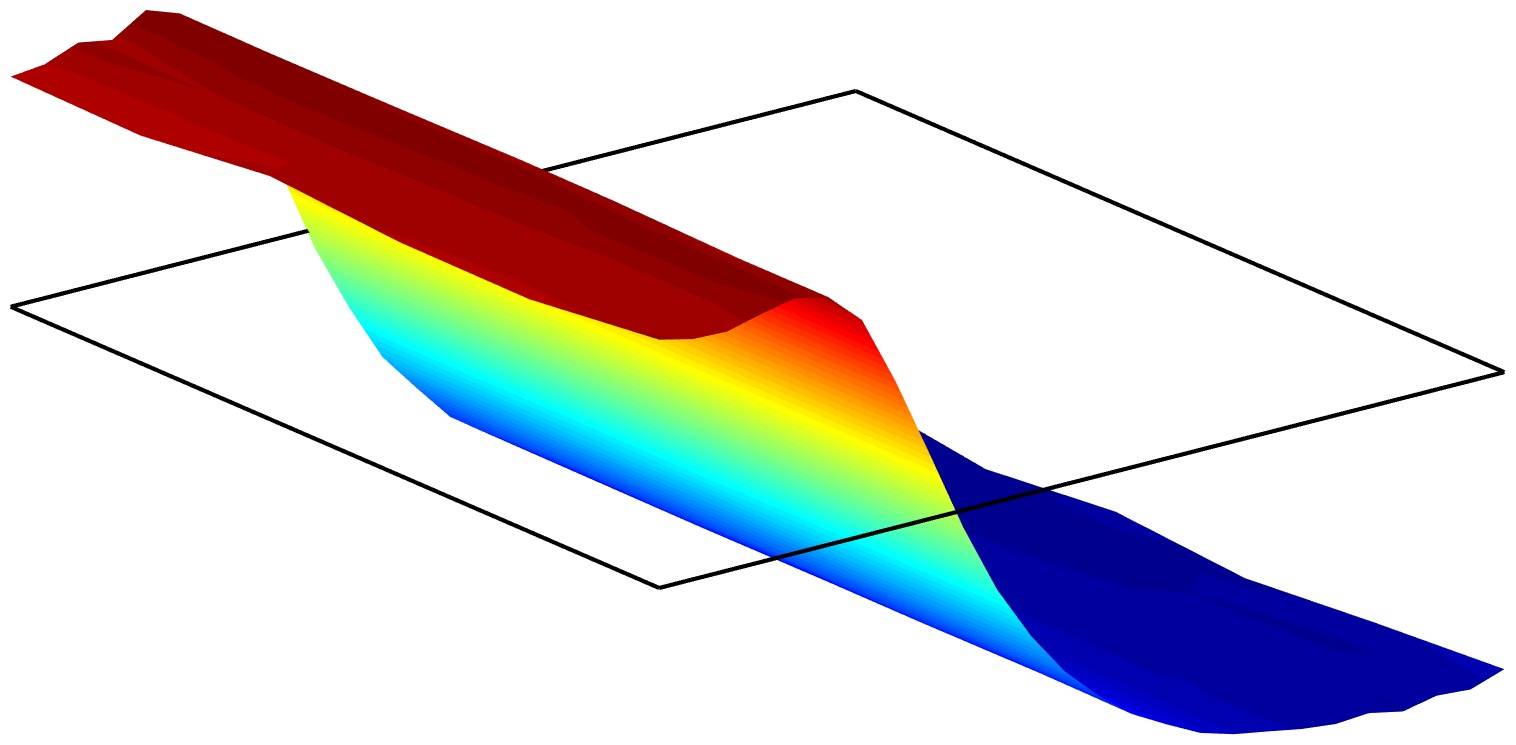
This example models a moving wave in a pool of shallow water. Although these types of fluid flows are governed by the full three-dimensional Navier-Stokes equations, they can be simplified with a two dimensional approximation, where the z-dimension is replaced with a variable h for the unknown free surface height relative to a mean level H. These equations, Saint-Venant shallow water equations, in the non-conservative form read
\[ \left\{\begin{array}{;’} \ \frac{\partial h}{\partial t} + (u\frac{\partial h}{\partial x} + v\frac{\partial h}{\partial y} ) + (h+H)(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}) = 0 \\\\ \frac{\partial u}{\partial t} + (u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} ) = -g\frac{\partial h}{\partial x} \\\\ \frac{\partial v}{\partial t} + (u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} ) = -g\frac{\partial h}{\partial y} \end{array}\right. \]
This model is available as an automated tutorial by selecting Model Examples and Tutorials… > Classic PDE > Shallow Water Equations from the File menu, viewed as a video tutorial below. Or alternatively, follow the linked step-by-step instructions.