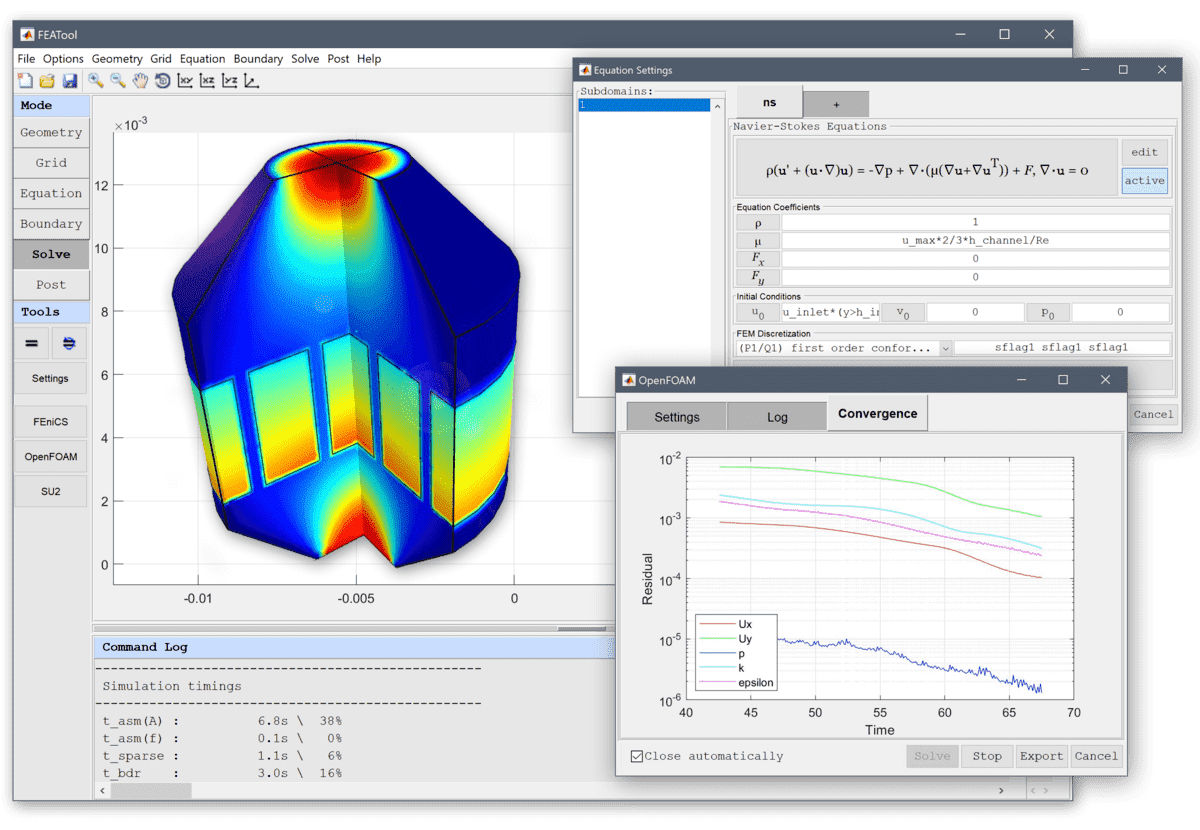
Black-Scholes Equation
Black-Scholes Equation
This is an example showing how to define a custom parital differential equation (PDE) equation model in the FEATool Multiphysics. In this case the Black-Scholes model equation, which is used in financial analytics to model derivatives and options pricing. The non-linear partial differential equation to be solved reads …
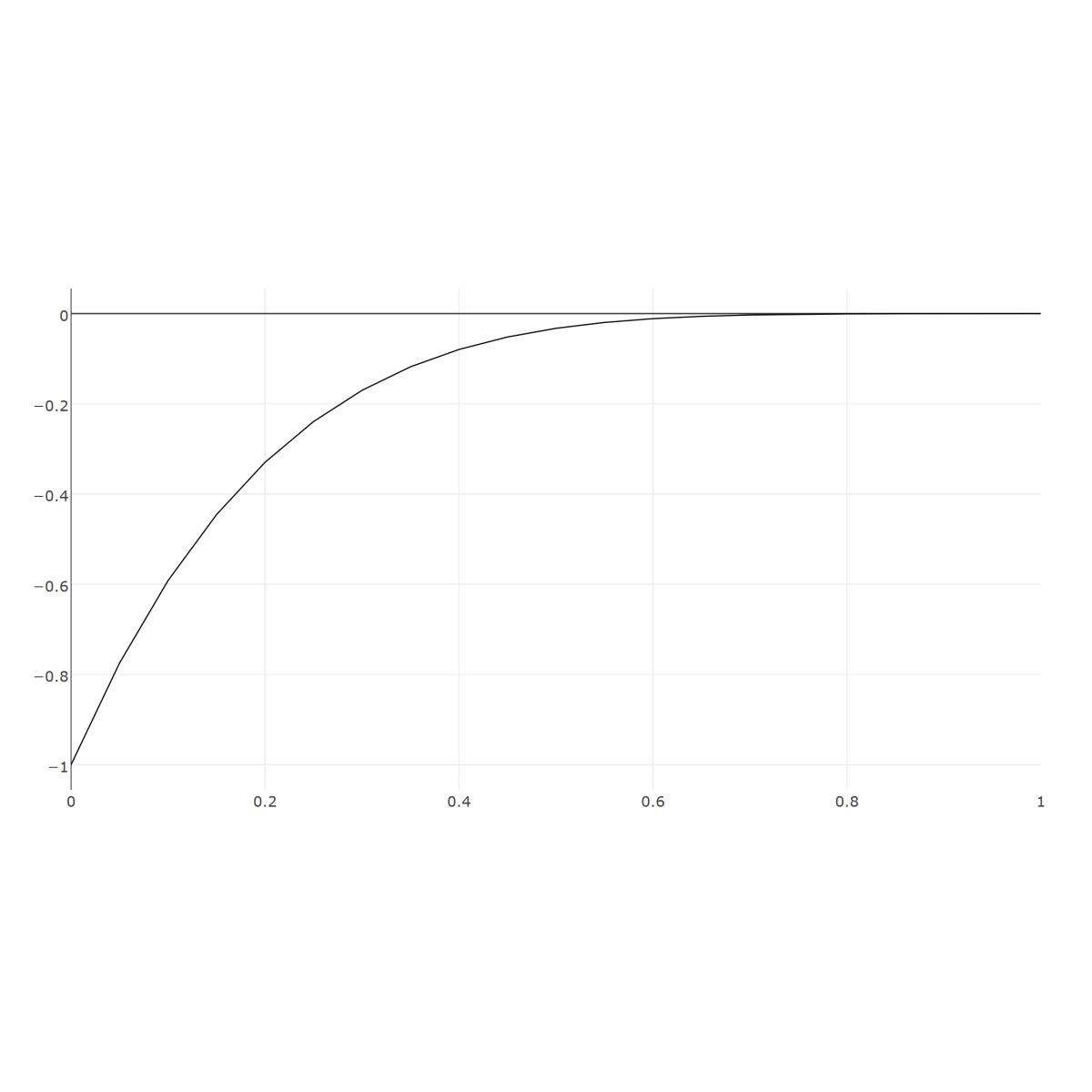
Poisson Equation
Poisson Equation
The classic Poisson equation is one of the most fundamental partial differential equations (PDEs). Although one of the simplest equations, it is a very good model for the process of diffusion and comes up in many applications (for example fluid flow, heat transfer, and chemical transport). It is therefore fundamental …
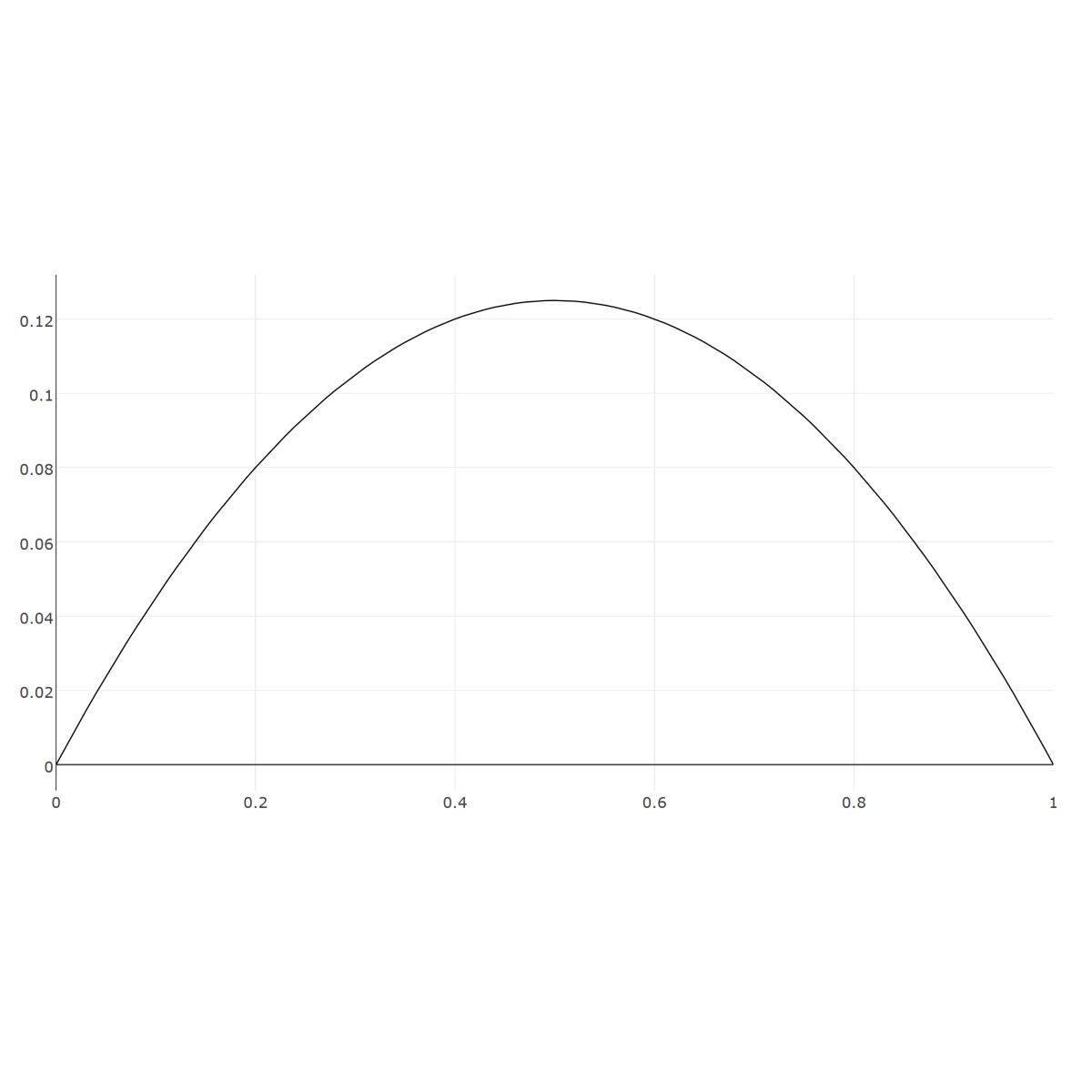
Poisson Equation with a Point Source
Poisson Equation with a Point Source
The classic Poisson equation is one of the most fundamental partial differential equations (PDEs). Although one of the simplest equations, it is a very good model for the process of diffusion and comes up again and again in many applications such as in fluid flow, heat transfer, and chemical transport. This example …
Resonance Frequencies of a Room
Resonance Frequencies of a Room
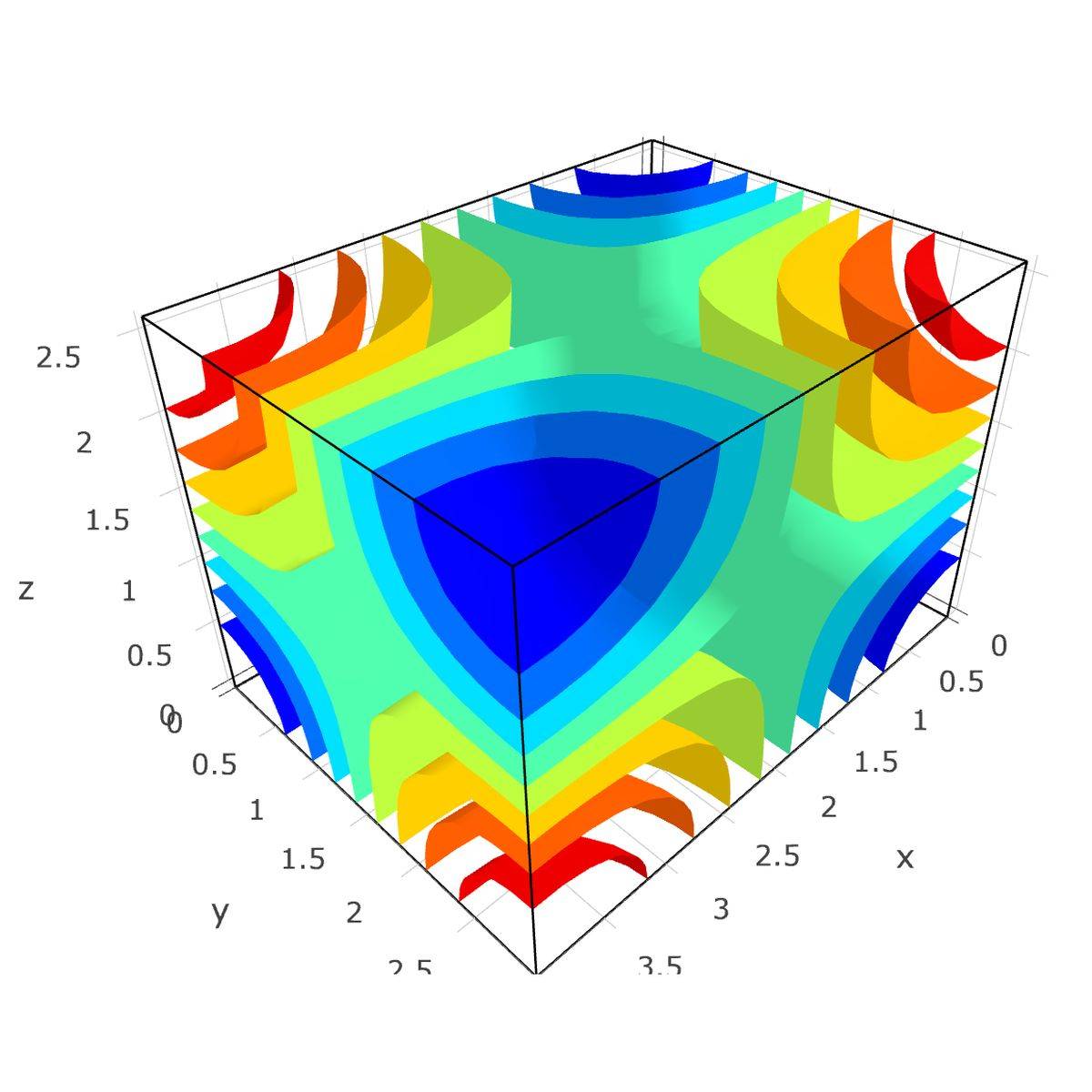
This example studies the resonance frequencies of an empty room by using the Helmholtz equation for the time-harmonic pressure field Δp + k2 = 0 The resulting eigenmodes can be compared to and validated against the analytical solution for the resonance frequencies of a boxed enclosure, that is f = c/2*√( (i/lx)2 …
Shallow Water Equations
Shallow Water Equations
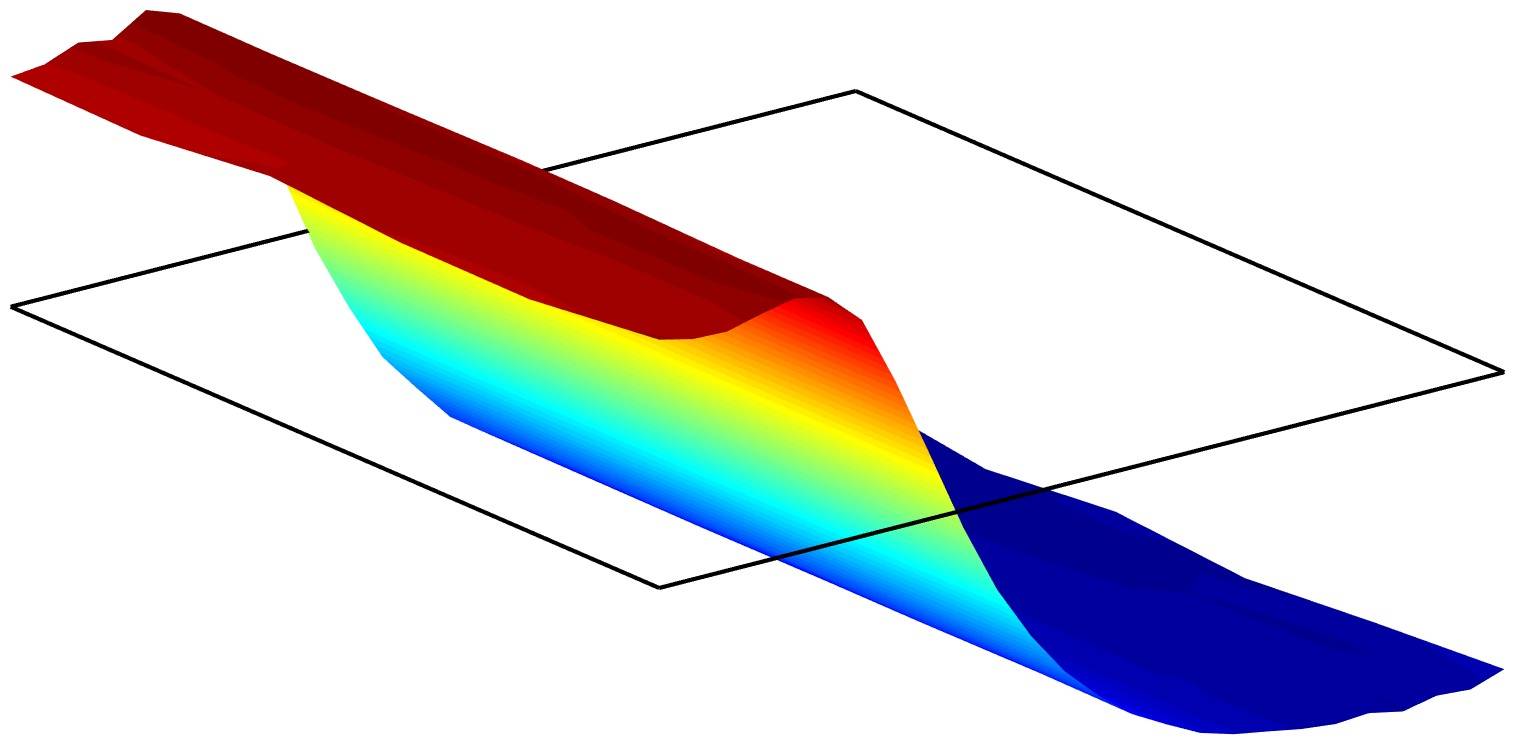
This example models a moving wave in a pool of shallow water. Although these types of fluid flows are governed by the full three-dimensional Navier-Stokes equations, they can be simplified with a two dimensional approximation, where the z-dimension is replaced with a variable h for the unknown free surface height …
Vibrations of a Circular Membrane
Vibrations of a Circular Membrane
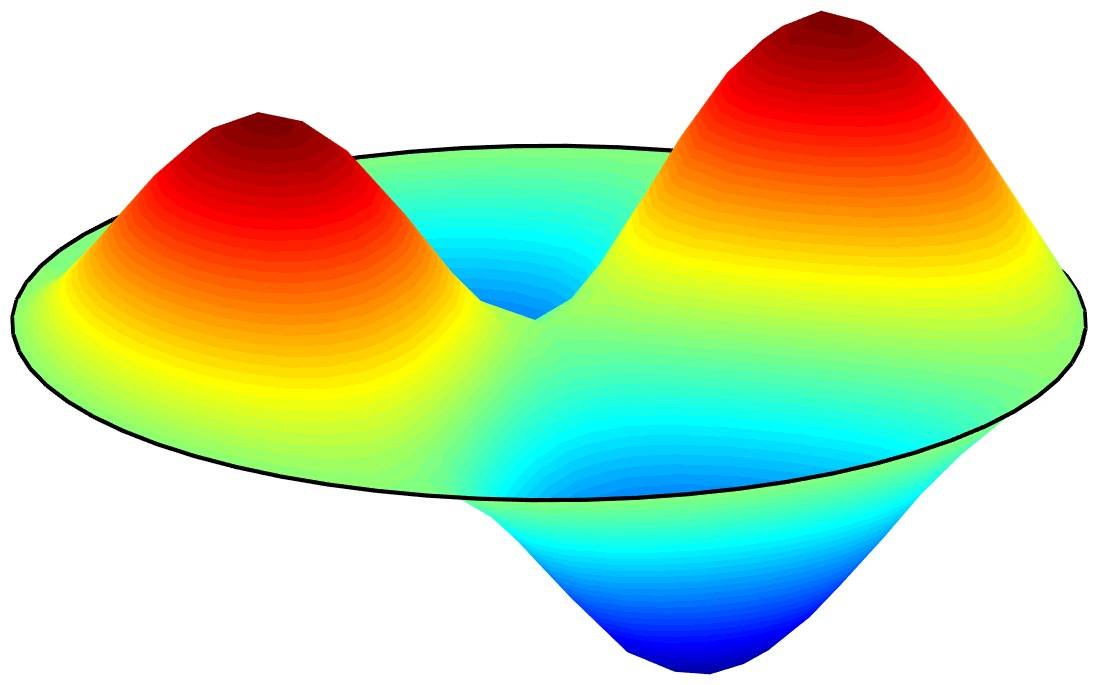
This example computes the the vibration modes, eigenvalues, and frequencies for a circular drum or membrane. The membrane is modeled by the unit circle and assumed to be attached to a rigid frame. The Poisson PDE equation is used with the Eigenvalue solver to compute the solution. This model is available as an …
Wave Equation on a Circle
Wave Equation on a Circle
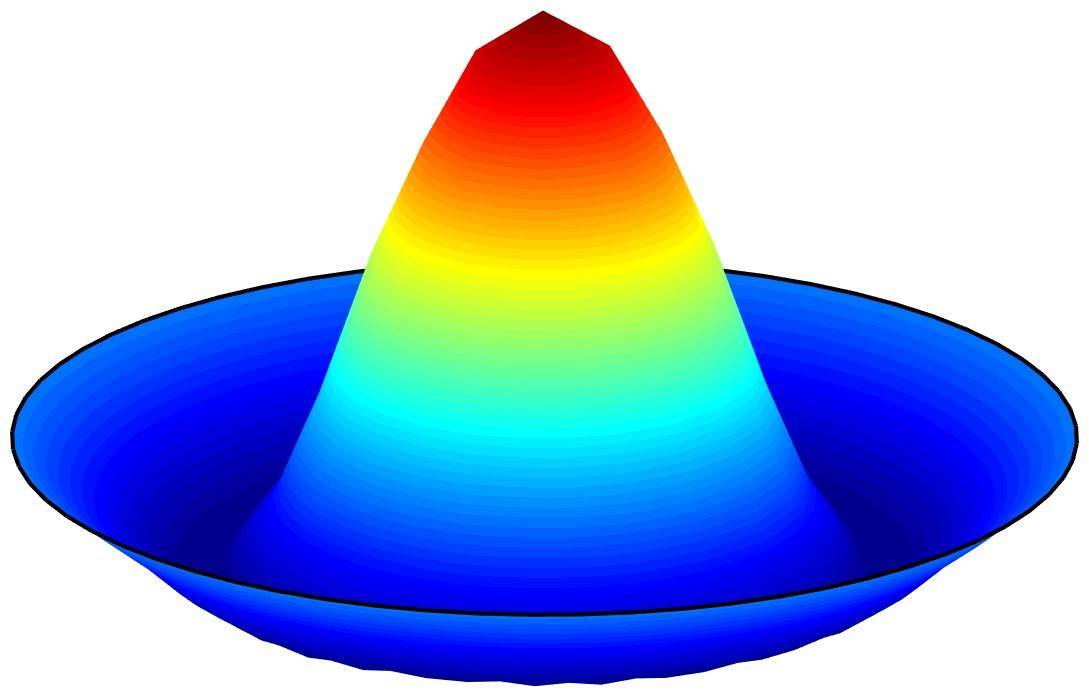
This tutorial explains how to set up and solve a generalized wave equation model on a circle, like for example for a drum or membrane, and then tracks how the initial parabolic deformed state will affect the resulting shape. The wave equation is one of the classic hyperbolic partial differential equations (PDE) of the …