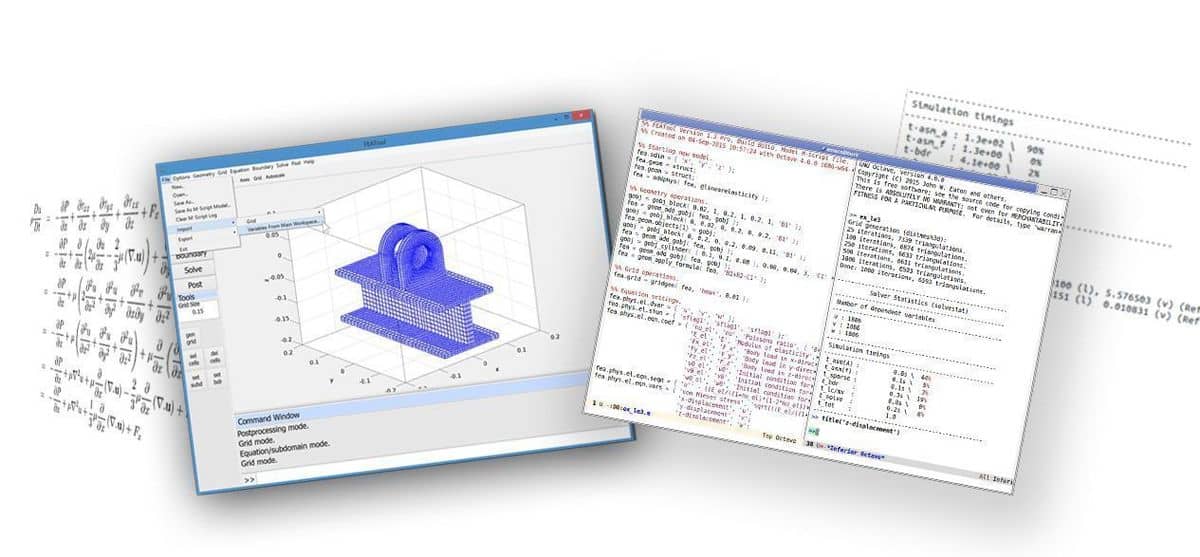
FEATool Multiphysics is unique in that it allows several different ways for users to work with FEM modeling and simulation. The whole spectrum from using the high-level graphical user interface down to low-level access of the fundamental matrices of the underlying finite element FEM discretization is possible. On top of this, since FEATool is written in m-script code, it can be extended and combined with MATLAB toolboxes and custom m-file scripts and functions. This post explains the following four different ways of working with FEATool
1. Graphical User Interface (GUI)
2. Pre-defined physics modes
3. Weak FEM equation formulation
4. Direct matrix assembly
where the last three approaches involve eschewing the GUI for the MATLAB command lines and m-script files.
Graphical User Interface (GUI)
Designed with ease of use in mind, the graphical user interface or GUI is usually the first way one works with FEATool.
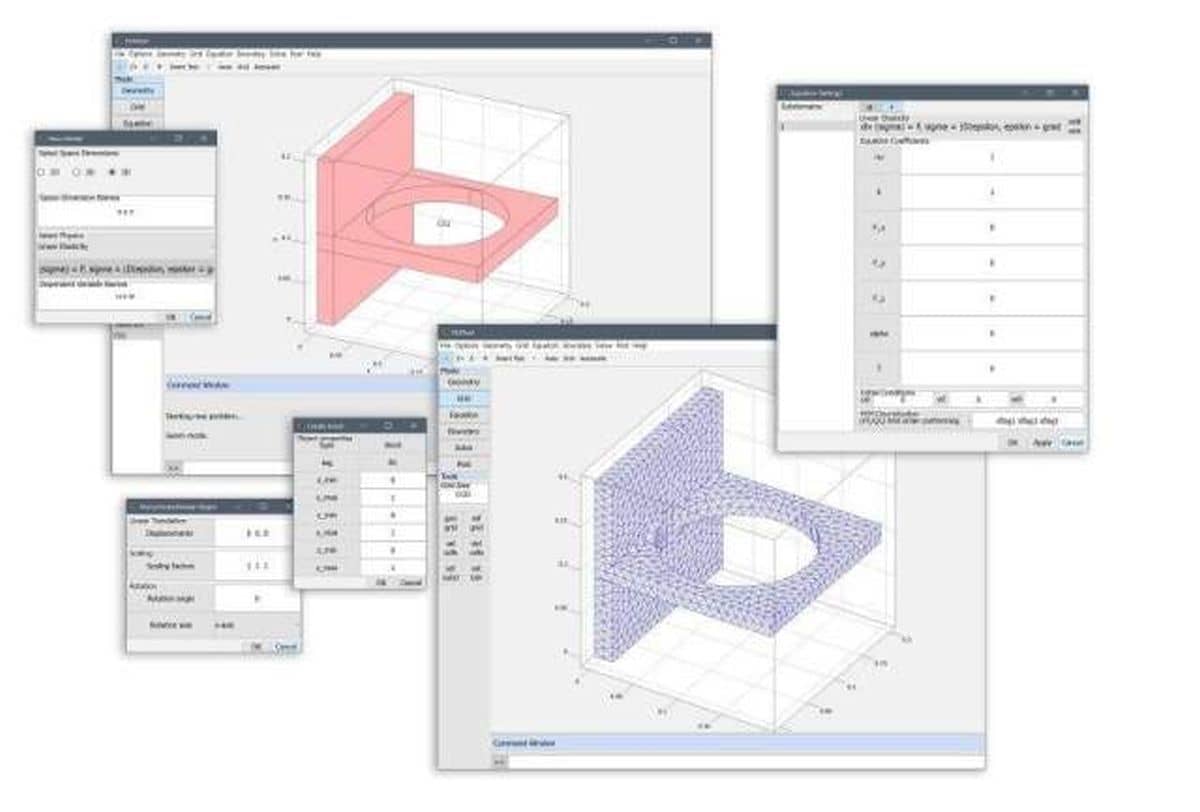
Although simple in nature, the FEATool GUI allows for some powerful features that can be utilized to extend code functionality.
It is for example possible to import and export fea data structs the
GUI and MATLAB main command line workspaces by using the corresponding
Export… and Import… menu options under the File menu.
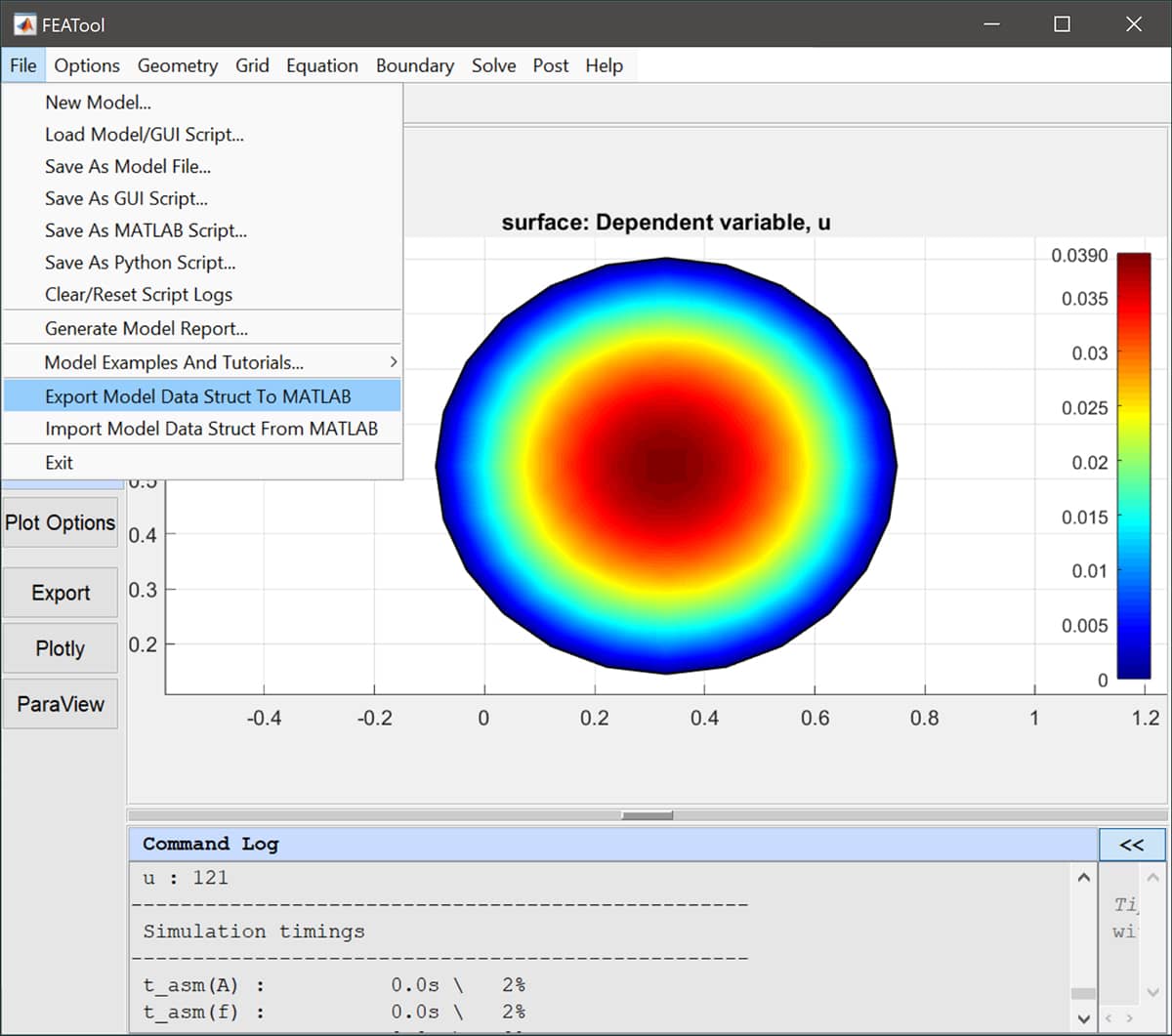
Pre-defined physics modes
The first step in working with MATLAB command line and m-script FEATool models is generally to use the pre-defined physics modes. A good way to understand and learn how FEATool script models are built up and constructed is to use the Save As M-Script Model… option instead of the binary .fea format file.
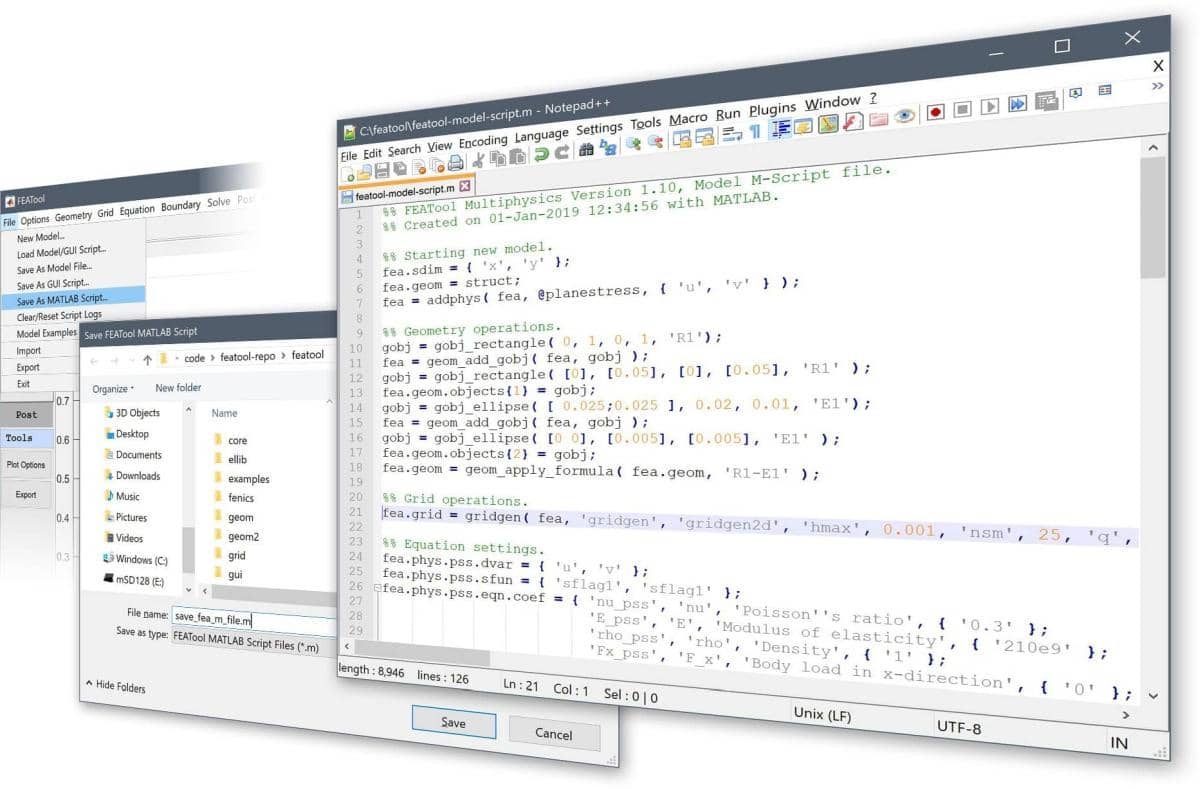
The output .m model source files can be opened in any text editor and the shown output corresponds directly with how the model was constructed in the GUI. Everything from the geometry definition, to solving and postprocessing has corresponding MATLAB function commands.
An example of solving the Poisson equation for a unit circle defined
with the Poisson physics mode can be found in the tutorial section of
the FEATool documentation As can
be seen in the example code, the physics modes are stored in the
fea.phys field of the fea model definition struct. The
actual strong PDE formulation is defined in the seqn
sub-field, in this case
fea = addphys( fea, @poisson );
fea.phys.poi.eqn.seqn = 'dts_poi*u' - d_poi*(ux_x + uy_y) = f_poi'
PDE equation coefficients can be specified as
fea.phys.poi.eqn.coef = { 'dts_poi' [] [] { 1 } ;
'd_poi' [] [] { 1 } ;
'f_poi' [] [] { 1 } ;
'u0_poi' [] [] { 0 } };
where u0_poi is the initial condition for the dependent variable u
as defined in fea.phys.poi.dvar. Similarly Dirichlet and
Neumann boundary conditions can be prescribed through the bcr_poi
and bcg_poi coefficients, respectively
fea.phys.poi.bdr.sel = 1;
fea.phys.poi.bdr.coef = ...
{ 'bcr_poi' [] [] [] [] [] { 0 } ;
'bcg_poi' [] [] [] [] [] { 1 } };
Lastly, the command parsephys
fea = parsephys( fea );
parses the equations in all the fea.phys structs and
enters the corresponding weak finite element formulations into the
global fea.eqn and fea.bdr multiphysics
fields.
Weak FEM equation formulation
If one prefers to directly work with the FEM weak formulations this is
also possible as shown here for
the same Poisson problem as above. Note how there is no
phys field or call to parsephys necessary when directly
prescribing the fea.eqn and fea.bdr fields
fea.eqn.a.form = { [2 3; 2 3] };
fea.eqn.a.coef = { [1 1] };
fea.eqn.f.form = { 1 };
fea.eqn.f.coef = { 1 };
n_bdr = max(fea.grid.b(3,:));
fea.bdr.d = cell(1,n_bdr);
[fea.bdr.d{:}] = deal(0);
fea.bdr.n = cell(1,n_bdr);
Direct matrix assembly
Finally, for advanced FEM users it is entirely possible to use the
core finite element assembly routines
assemblea and
assemblef to assemble the
system matrix and right hand side/load vector after which they can be
directly manipulated. Again, the corresponding Poisson problem example
is described in
the CLI Poisson equation tutorials.
The source code for the matrix and source term vector assembly looks
like the following
form = [2 3;2 3];
sfun = {'sflag1';'sflag1'};
coef = [1 1];
i_cub = 3; % Numerical quadrature rule to use.
[vRowInds,vColInds,vAvals,n_rows,n_cols] = ...
assemblea( form, sfun, coef, i_cub, ...
fea.grid.p, fea.grid.c, fea.grid.a );
A = sparse( vRowInds, vColInds, vAvals, n_rows, n_cols );
form = [1];
sfun = {'sflag1'};
coef = [1];
i_cub = 3;
f = assemblef( form, sfun, coef, i_cub, ...
fea.grid.p, fea.grid.c, fea.grid.a );
Note that here we have to directly prescribe boundary conditions to the system matrix and right hand side vector.
Altogether one can see that FEATool together with MATLAB allows for many possibilities to set up, perform, and analyze multiphysics FEM simulations.