
OpenFOAM is a well known and popular open-source Computational Fluid Dynamics (CFD) solver, and features a large selection of solvers for laminar, and turbulent, incompressible, and compressible flow regimes as well as complex multi-physics applications including heat transfer, chemical reactions, etc. As such it widely used in both in industry and academia, for example in automotive engineering applications and in F1 racing to model and optimize aerodynamics performance [1,2].
Since defining and setting up simulations in OpenFOAM is entirely script based, using text based dictionaries, new users can often find it intimidating and frustrating to learn and start doing CFD simulations. As an alternative, FEATool Multiphysics™ now features an easy-to-use Graphical User Interface (GUI) for setting up and running simulations with OpenFOAM.
Get started with OpenFOAM and CFD simulations in minutes!
With a fully integrated GUI and built-in pre-processing, automatic mesh generation, pre-defined flow solvers, postprocessing and visualization, setting up and running OpenFOAM fluid dynamics simulations with the FEATool Multiphysics and/or CFDTool™ toolboxes has never been easier or more convenient.
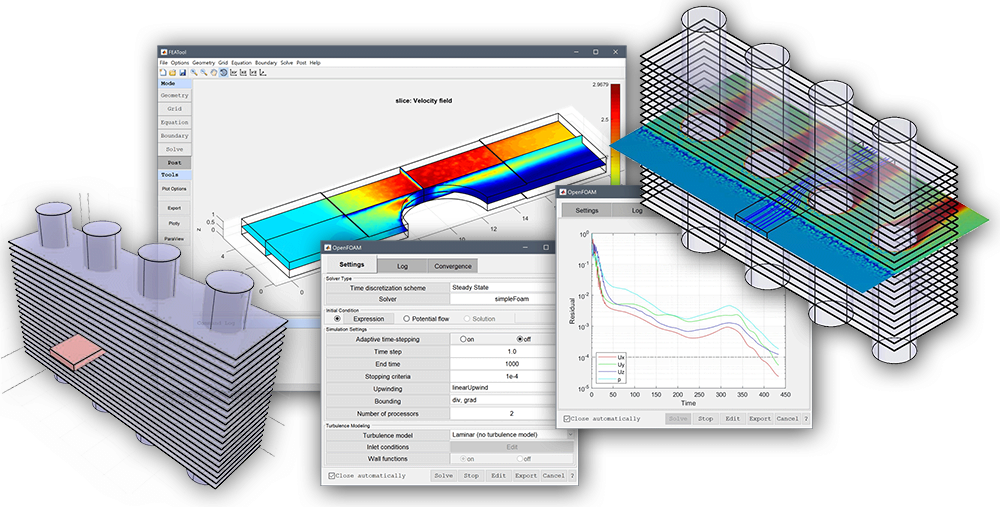
Easy-to-Use GUI for OpenFOAM
The FEATool Multiphysics and CFDTool toolboxes allows for defining fluid mechanics and heat transfer simulation cases and setting up corresponding OpenFOAM case files, as well as running and monitoring simulations without ever having to leave the GUI. The toolboxes include a wide range of features and capabilities, such as
- Built-in Computer Aided Design (CAD) tools for 2D and 3D solid geometry modeling
- Define geometry models with a simple CAD UI
- Import geometries from STEP, IGES, and STL CAD files
- Automatic unstructured mesh generation
- Simple and easy one-click mesh and grid generation
- 2D to 3D mesh conversion for two-dimensional, axisymmetric, and swirl flow models
- Support for several mesh generators such as GMSH, Netgen, TetWild, and Triangle
- Automatic handling of regions with multiple domains
- Dedicated UI and solver control panel for OpenFOAM
- Support for incompressible, compressible, laminar and turbulent flow solver applications
- Simulations with conjugate heat transfer applications with natural and forced convection
- Built-in editor for modifying and customizing OpenFOAM case files and dictionaries
- Export and import of external case files and dictionaries
- Automatic decomposition and handling of parallel domains and computations
- Solver control, solution, and residual monitoring directly in the GUI
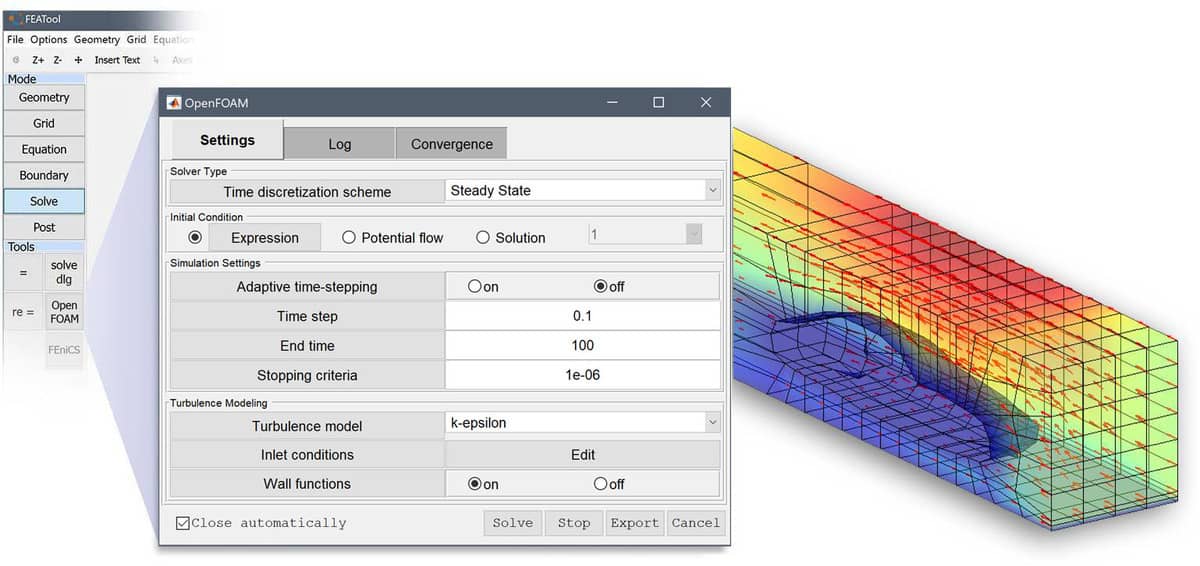
- Integrated visualization, postprocessing, and analysis of results for CFD simulations
- Share results with colleagues directly online with export to ParaView, VTK, and Plotly Html web formats
- Full cross-platform GUI support for Microsoft Windows, Linux, and MacOS
OpenFOAM & CFD Simulations Made Easy!
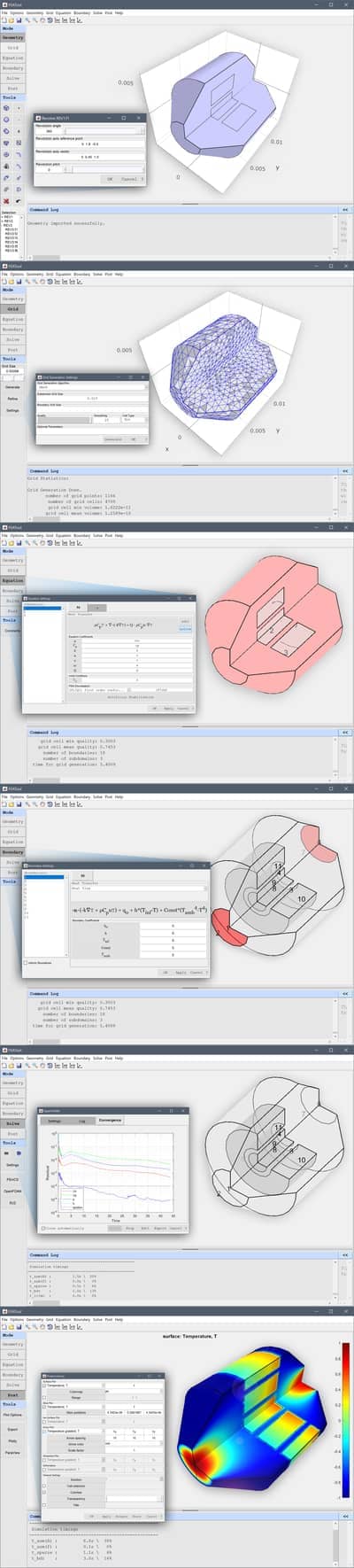
With the toolbox and interface integrations for OpenFOAM, complexities of setting up advanced and parallel CFD simulations is as much as possible now completely automated. The toolbox can automatically mesh, define and set up corresponding case files, parametrize and solve the flow cases, so that users can save work and effort, instead putting more time on result analysis and reporting.
The GUI can either be used to run full fluid dynamics simulations, or used as a pre and post-processor for setting up, defining, and postprocessing simulations, as well as aid to learn the complex OpenFOAM dictionary syntax and defining case files with the export functionality.
OpenFOAM CFD Simulation Scripts
Moreover, as each action and operation made in the GUI corresponds to a specific toolbox function call (“button click and selection”), it also enables directly exporting and running CFD and OpenFOAM simulations as MATLAB scripts and integrate it with MATLAB as a CFD toolbox. This can be used to easily set up automated parametric simulation runs and parallel studies, and combining simulation models with all available MATLAB scripting functionality and toolboxes.
Furthermore, as every modeling step is recorded the UI, it can also be completely automated and played back, which is ideal for producing reproducible step-by-step CFD tutorials, as well as learning [5], and for producing educational teaching material [3,4].
Coupled Multiphysics & Multi-Solver CFD Simulations
The unique multi-solver capabilities of FEATool Multiphysics allows users to easily set up and run simulations combined and coupled with completely different physics solvers. This functionality makes it possible to use the most accurate and efficient solvers for different parts of a model, both from the fully integrated GUI and Command Line Interfaces (CLI).
One can for example use the CFD solvers OpenFOAM or SU2 for solving for the flow field, and couple it with the FEniCS or FEATool FEA solvers for simulation of temperature equations, chemical reactions, and more.
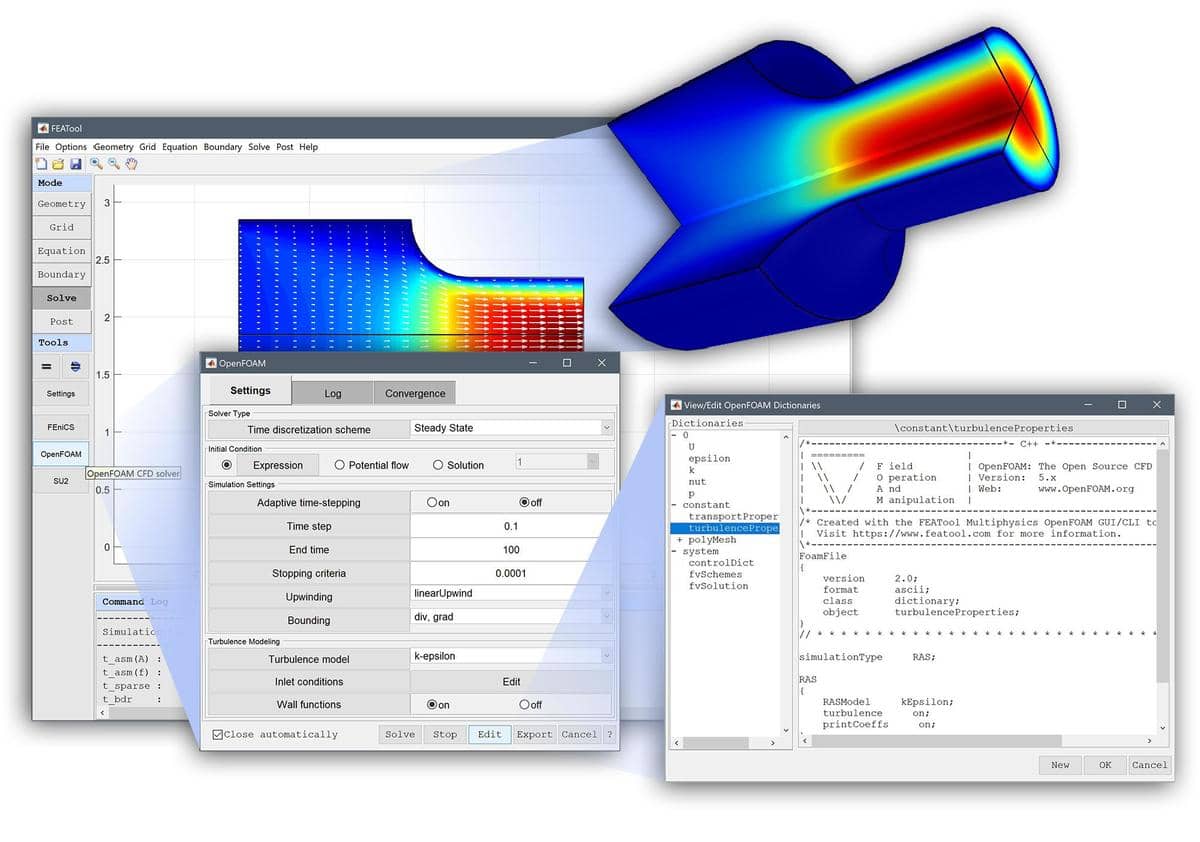
An example of the multi-solver simulation functionality is available as a CFD tutorial of modeling cooling via forced convection in a tube and fin heat exchanger. In this multi-simulation model the flow field and fluid dynamics is solved with OpenFOAM, after which the temperature field is solved with the built-in multi-physics solver (using the flow field previously computed with OpenFOAM).
Combined with the automatic parallel processing support, the multi-solver simulation functionality saves both computational time and memory, and enables solving more complex and larger scale models not previously possible.
Availability and Download
Please feel free to download and try FEATool Multiphysics and OpenFOAM GUI integration from the link below
If you use FEATool Multiphysics and/or CFDTool and find it useful in your work or studies please do share your models, modeling experience, and consider recommending the toolboxes to your colleagues and coworkers.
References
[1] Barbaschow A. F1 turns to AWS to develop 'next-gen' race car, zdnet innovation article, December 2, 2019.
[2] Aerodynamic Simulation of a 2017 F1 Car with Open-Source CFD Code, Journal of Traffic and Transportation Engineering 6, 155-163, 2018.
[3] Huang J.Y. Course on Partial Differential Equations and Multihysics Coupling Simulations, Labratory for optical studies of advanced materials, Chiao Tung University, Taiwan, 2020.
[4] Dechaumphai P. Numerical Methods & Computer Aided Engineering with MATLAB & ANSYS, Chulalungkorn University Press (CUP), 2598, 2023, ISBN: 978-974-03-4204-5.
[5] Kuzmin A.G. Using FEATool Multiphysics software for CFD Education, International Journal of Open Information Technologies, vol 12, no 1, 2024, ISSN: 2307-8162.