
|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|
This verification example considers a perfectly conducting sphere placed between two charged capacitor plates. An axisymmetric solution for the electrostatic potential is compared with a full 3D one, and verified against the analytical solution U(xi) = E0*(r3/xi2 - xi), where the electrical field is the potential difference divided by the distance between the plates Ei = dV/di.
In this example the conductive sphere is given a radius of 1 mm while the distance between the places is 1 cm. The area of the places is taken as 0.1 x 0.1 m and in axisymmetric coordinates a circle with equivalent area. The applied voltage is 20 V and dielectric permittivity of the medium ε = 5.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Electromagnetics > Conducting Sphere from the File menu. Or alternatively, follow the step-by-step instructions below.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Electromagnetics > Conducting Sphere from the File menu. Or alternatively, follow the step-by-step instructions below.
The axisymmetric case is considered first.
Select the Electrostatics physics mode from the Select Physics drop-down menu.
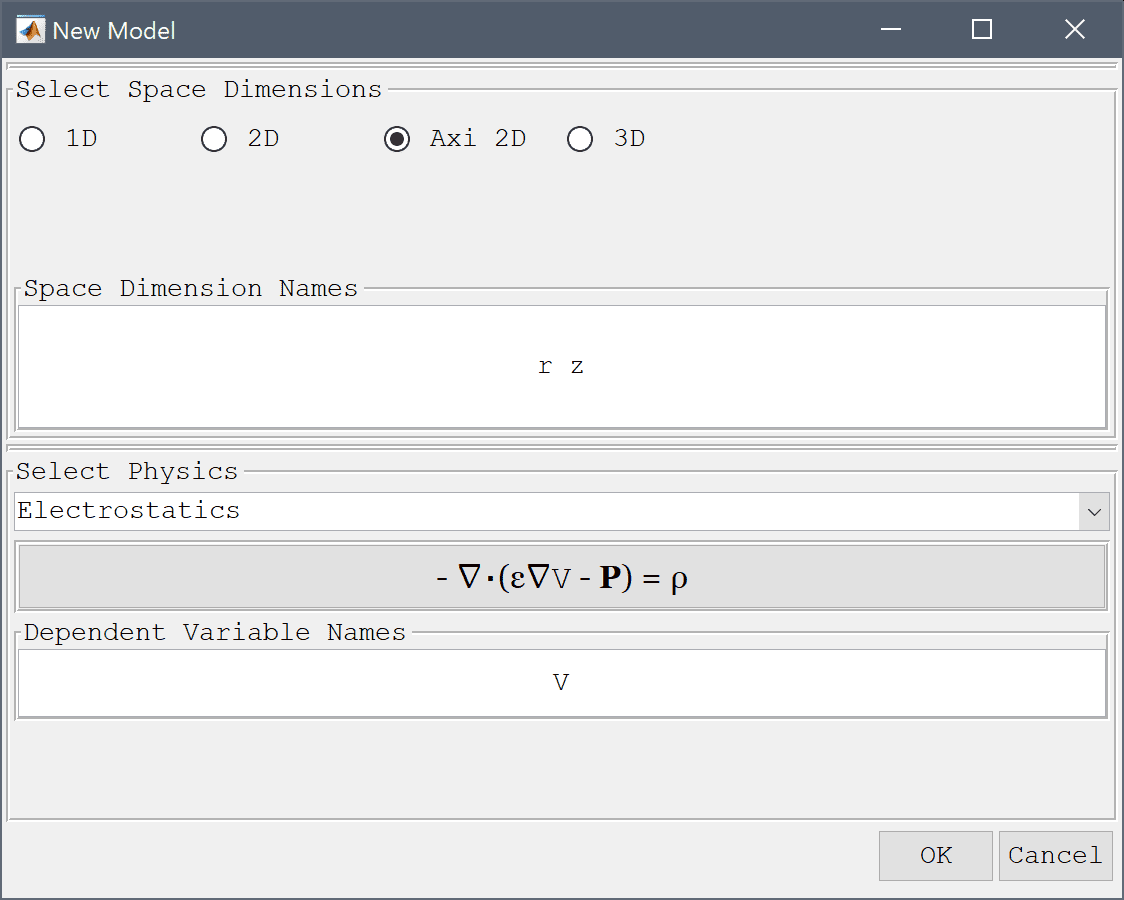
1e-3 into the radius edit field.-1e-3 into the xmin edit field.0 into the xmax edit field.-1e-3 into the ymin edit field.Enter 1e-3 into the ymax edit field.
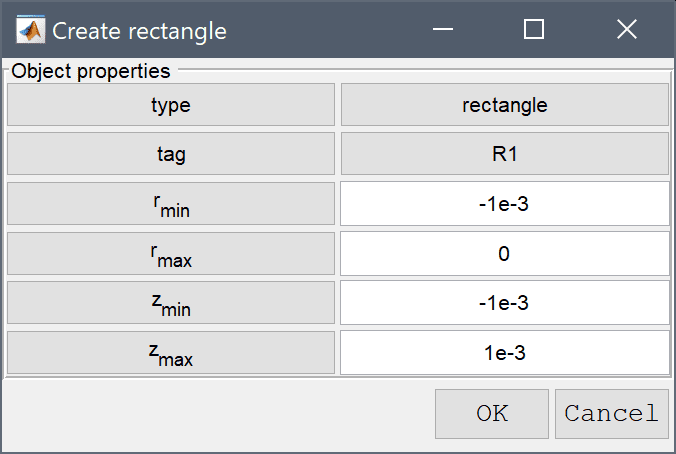
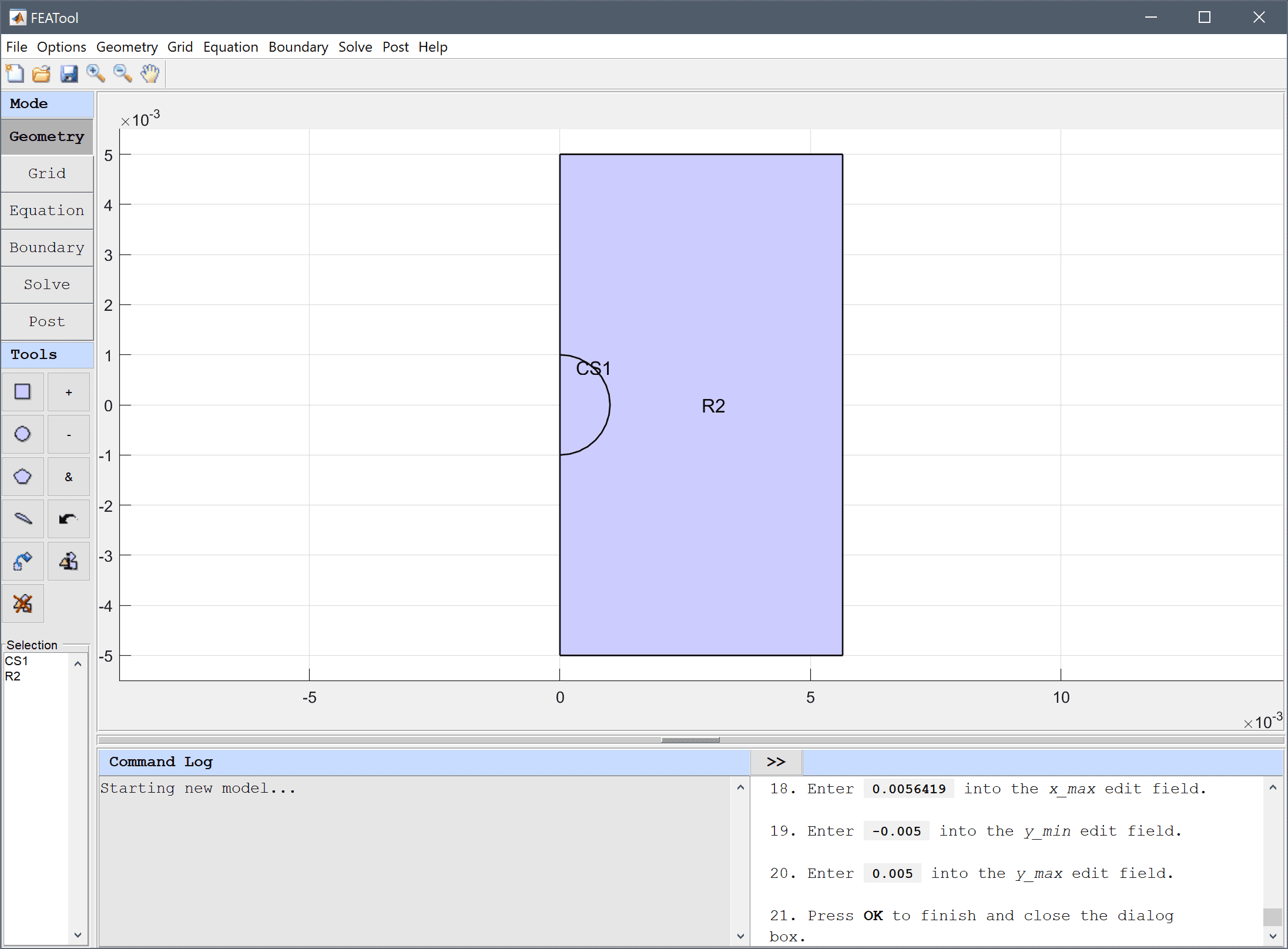
The max domain radius can be calculated to be 0.0056419 m to have an equivalent area of 1 cm squared.
0 into the xmin edit field.0.0056419 into the xmax edit field.-0.005 into the ymin edit field.Enter 0.005 into the ymax edit field.
Press OK to finish and close the dialog box.
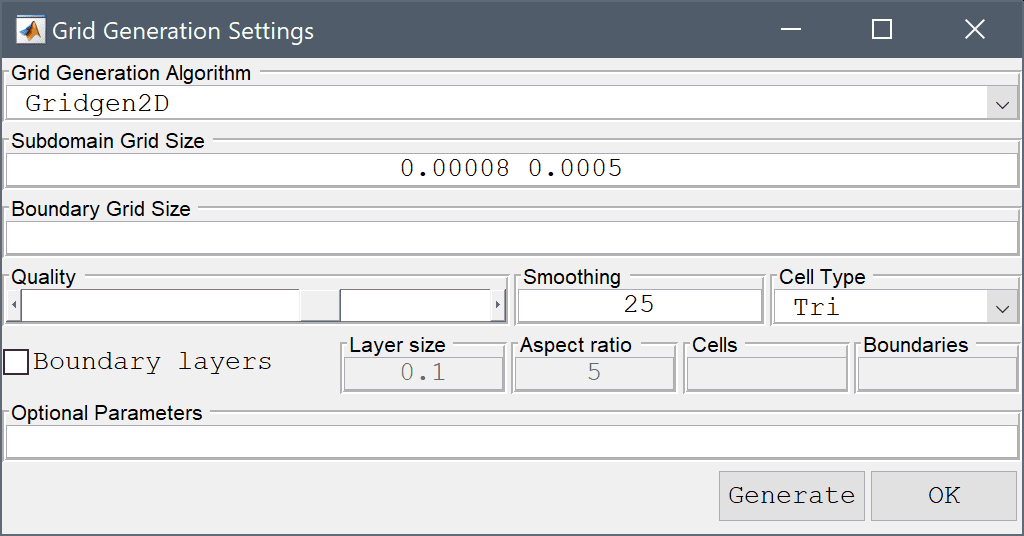
We can prescribe different grid sizes for different subdomains and boundaries. Here a smaller size is used for the sphere domain to locally increase the resolution and accuracy of the simulation.
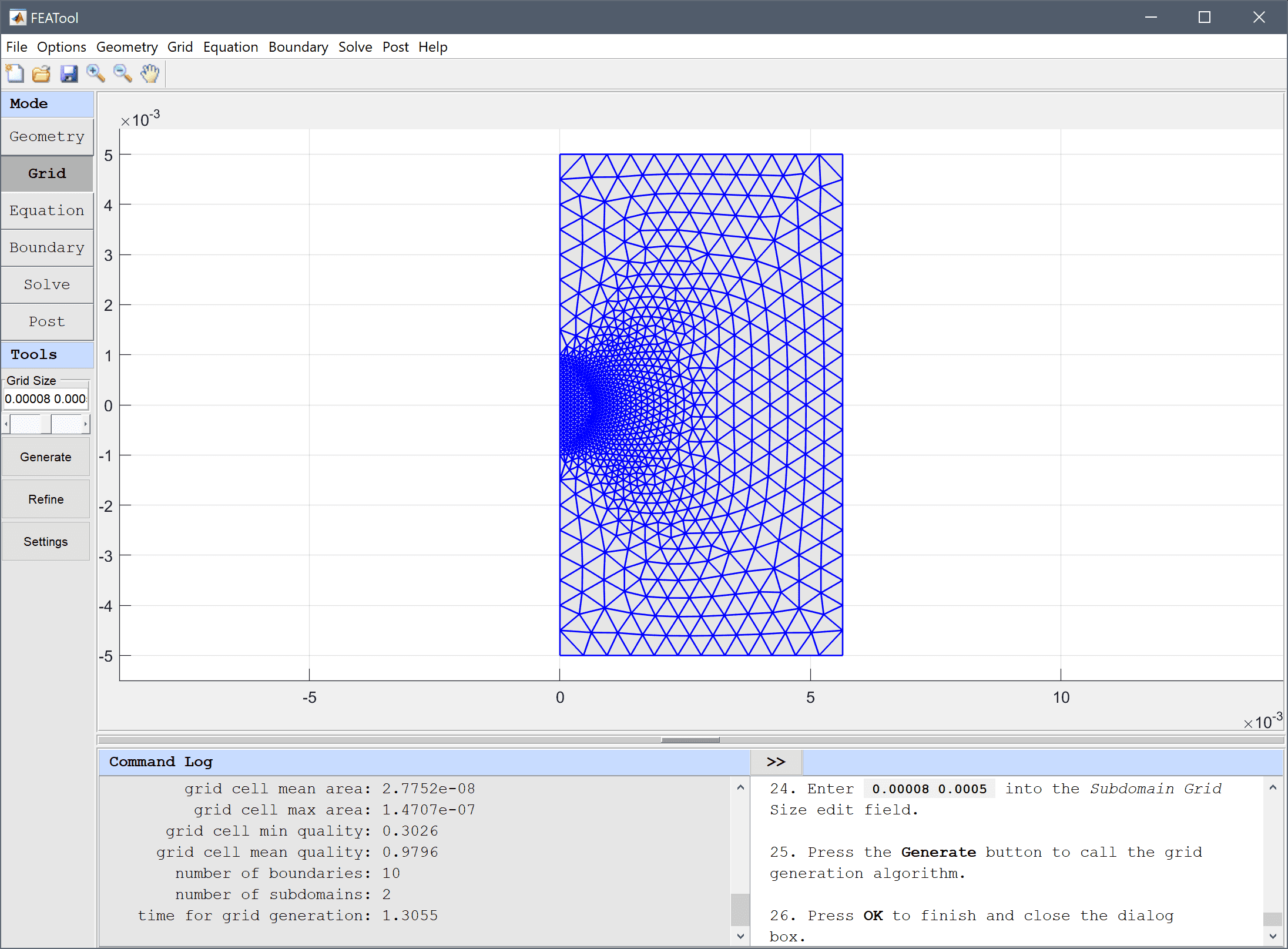
0.00008 0.0005 into the Subdomain Grid Size edit field.Press the Generate button to call the grid generation algorithm.
Press OK to finish and close the dialog box.
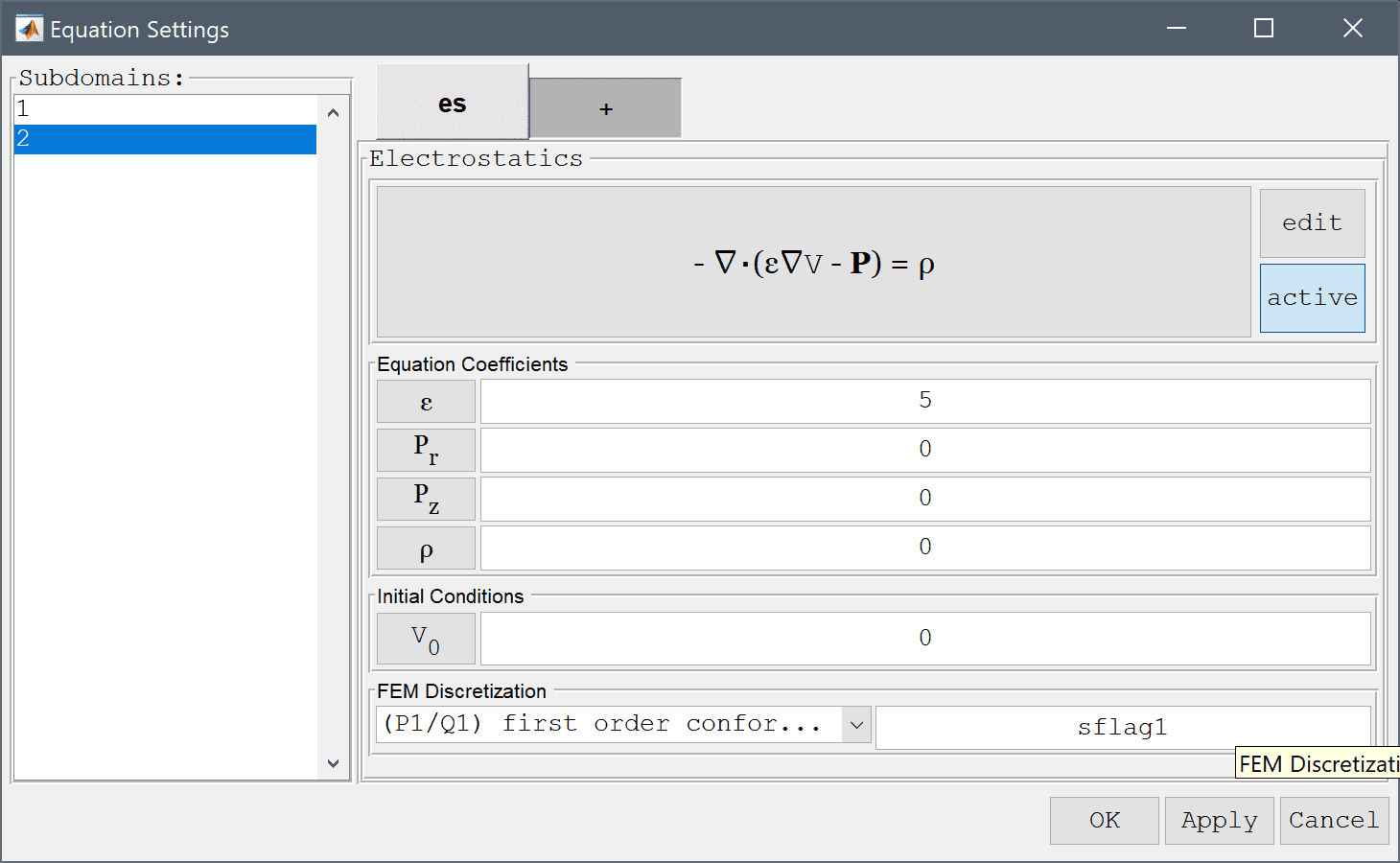
A domain with a very high permittivity can be used to represent a perfectly conducting region.
10000 into the Permittivity edit field.Enter 5 into the Permittivity edit field.
Enter 12 into the Electric potential edit field.
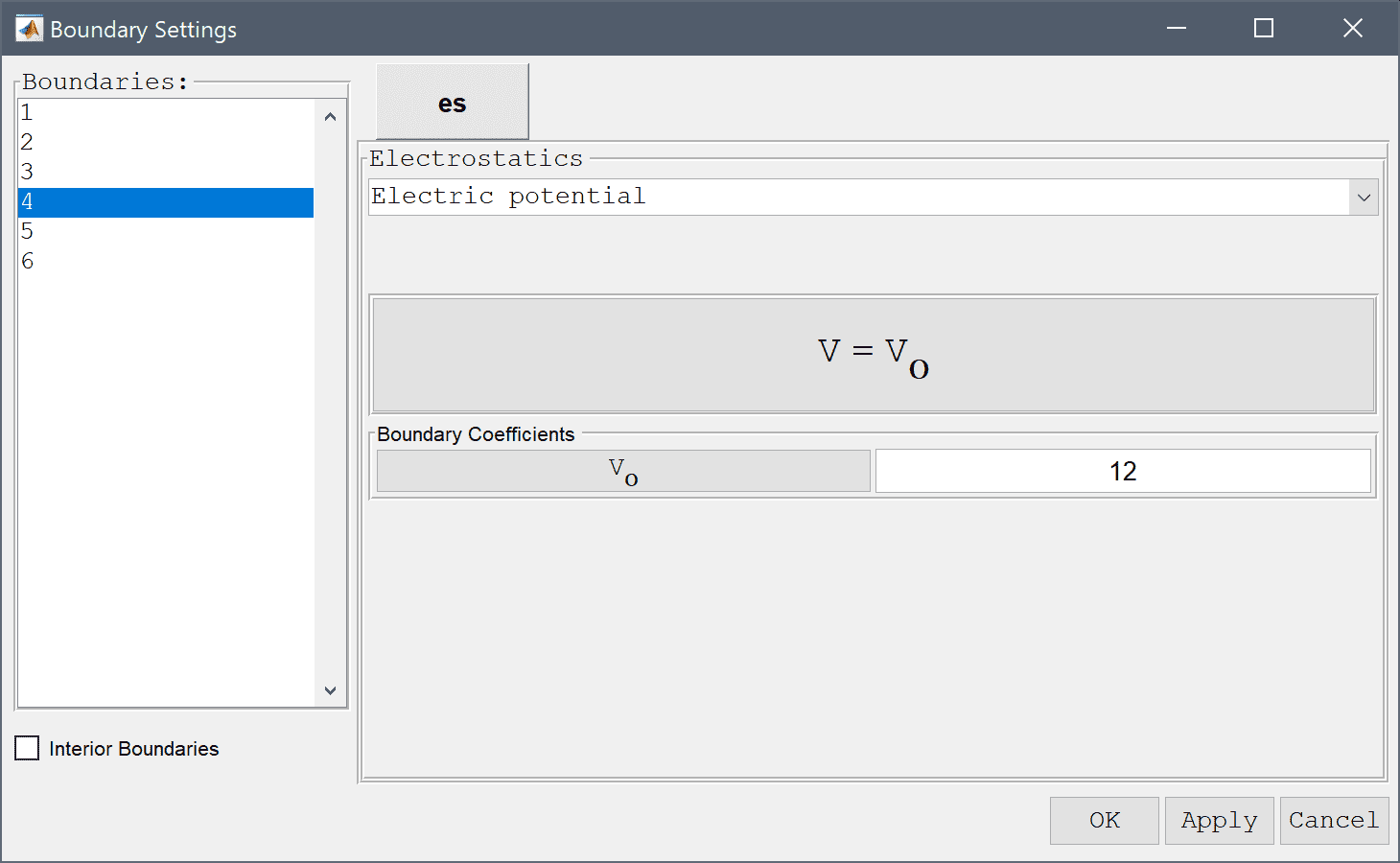
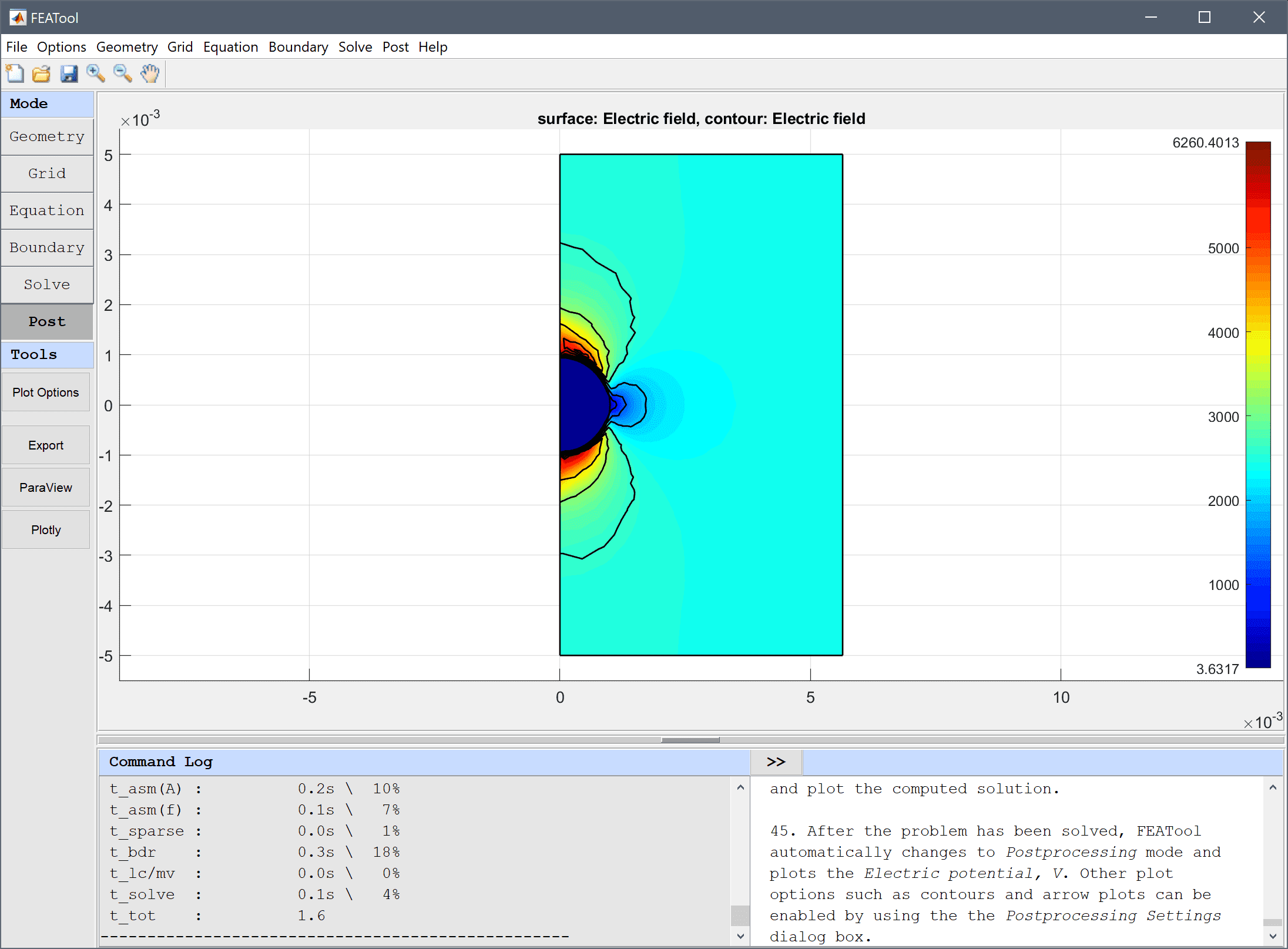
-12 into the Electric potential edit field.After the problem has been solved, FEATool automatically changes to Postprocessing mode and plot the Electric potential, V. Other plot options such as contour and arrow plots can be enabled by using the Postprocessing Settings dialog box.

Use the Line Evaluation postprocessing tool to plot the potential as a function of the radius.
The coordinates can be prescribed as a space or comma separated list of points, or a valid MATLAB expression resulting in a numeric scalar or vector.
zeros(1,100) into the Evaluation coordinates in r-direction edit field.Enter linspace(0,0.005,100) into the Evaluation coordinates in z-direction edit field.
Press the Apply button.
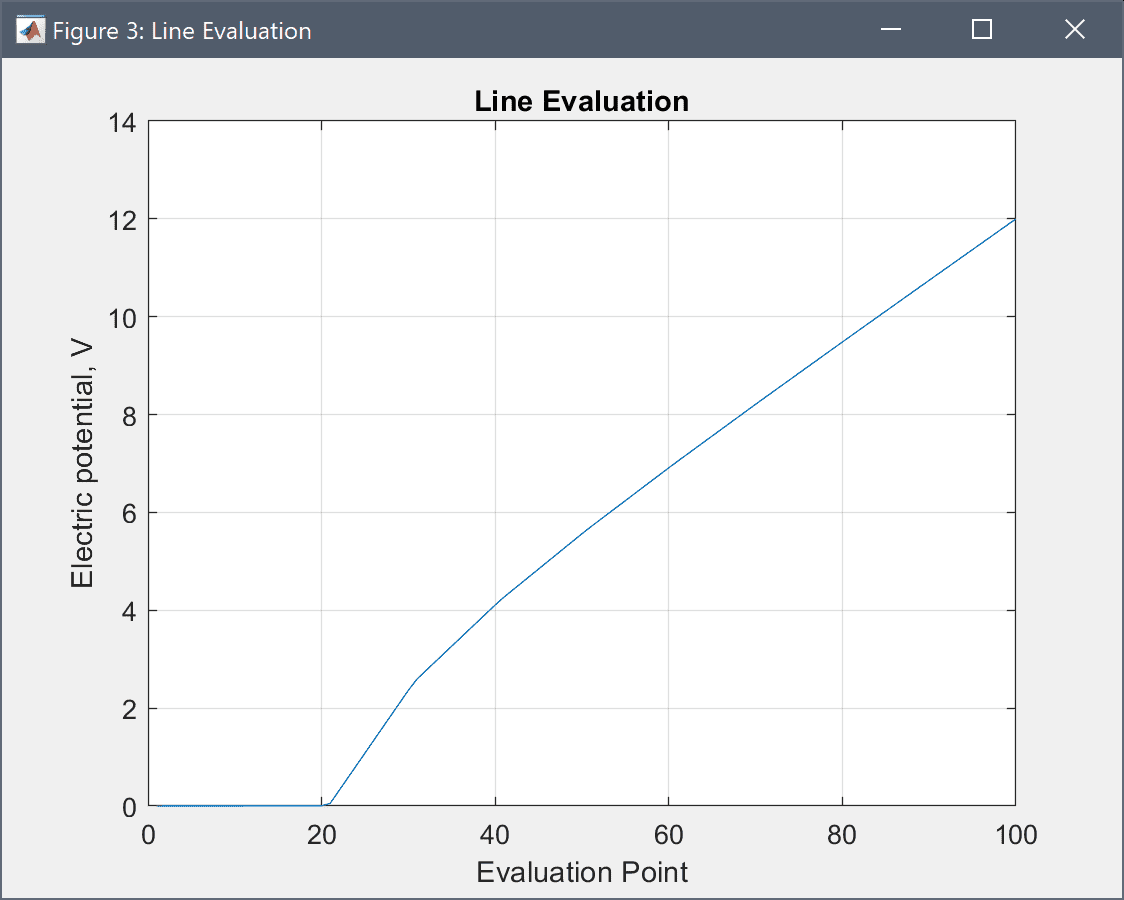
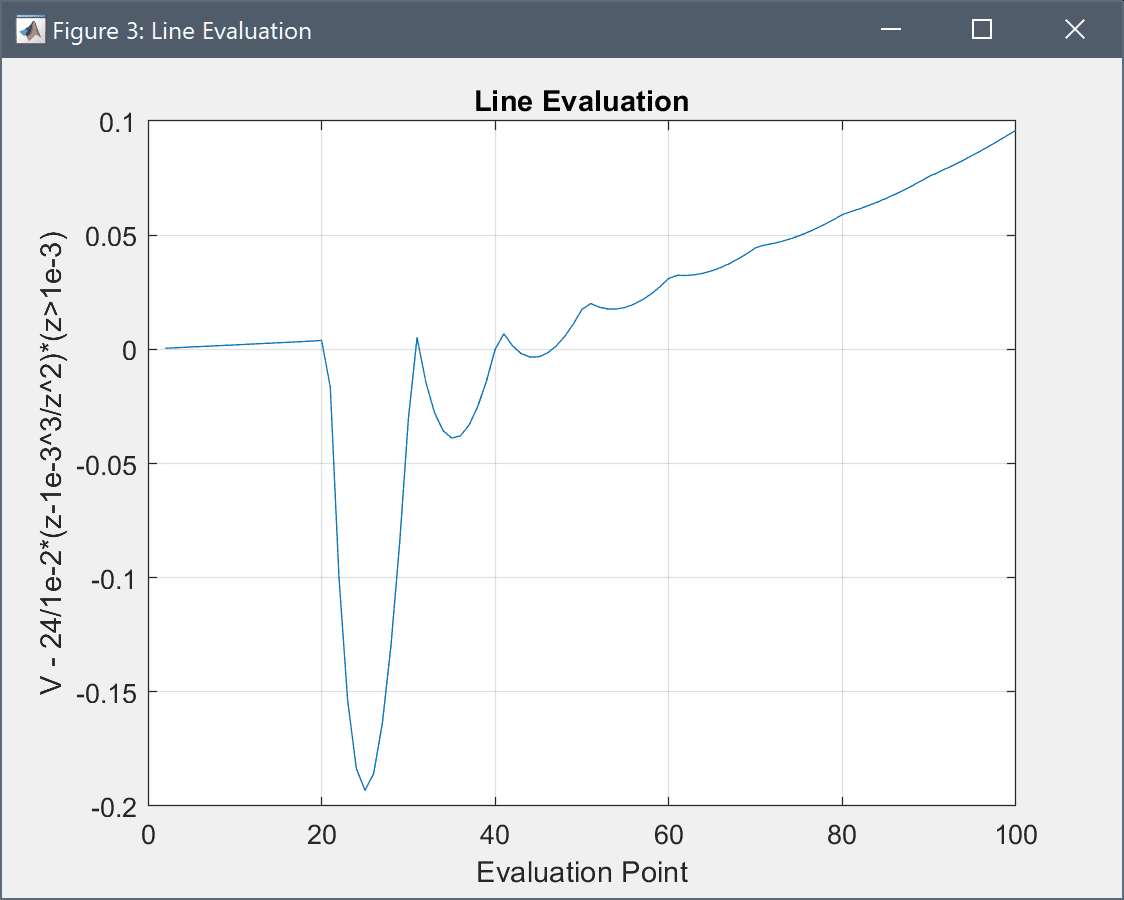
By plotting the difference between the computed potential and the analytical solution we can see how accurate the simulation is. Here we get a maximum error of about 0.1-0.2 V.
V - 24/1e-2*(z-1e-3^3/z^2)*(z>1e-3) into the edit field.Press the Apply button.
Next we switch to the equivalent model in full 3D with a block domain. The rest of the model setup is analogous to the axisymmetric case.
Select the Electrostatics physics mode from the Select Physics drop-down menu.
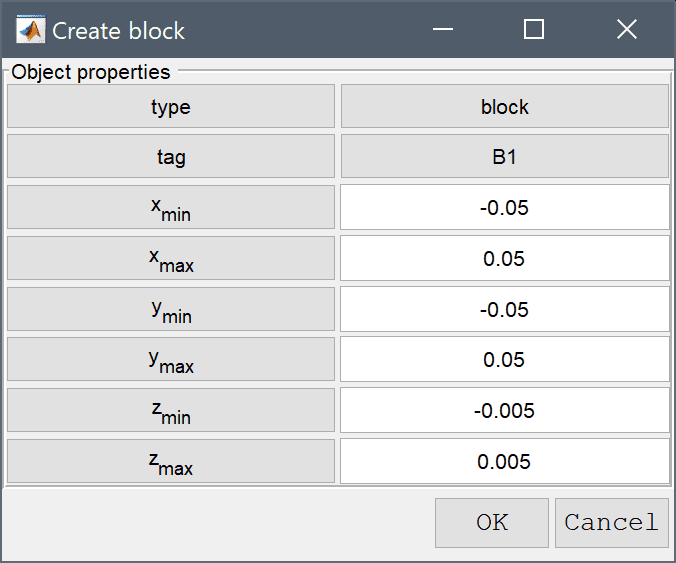
-0.05 into the xmin edit field.0.05 into the xmax edit field.-0.05 into the ymin edit field.0.05 into the ymax edit field.-0.005 into the zmin edit field.Enter 0.005 into the zmax edit field.
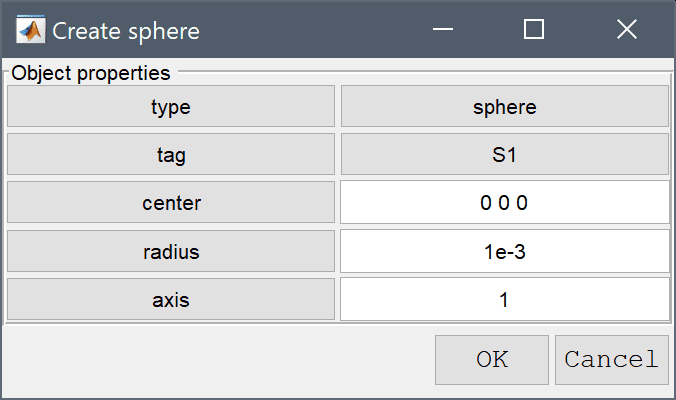
Enter 1e-3 into the radius edit field.
Press OK to finish and close the dialog box.
0.0002 0.0025 into the Subdomain Grid Size edit field.Press the Generate button to call the grid generation algorithm.
5 into the Permittivity edit field.Enter 10000 into the Permittivity edit field.
Enter 12 into the Electric potential edit field.
-12 into the Electric potential edit field.zeros(1,100) into the Evaluation coordinates in x-direction edit field.zeros(1,100) into the Evaluation coordinates in y-direction edit field.Enter linspace(0,0.005,100) into the Evaluation coordinates in z-direction edit field.
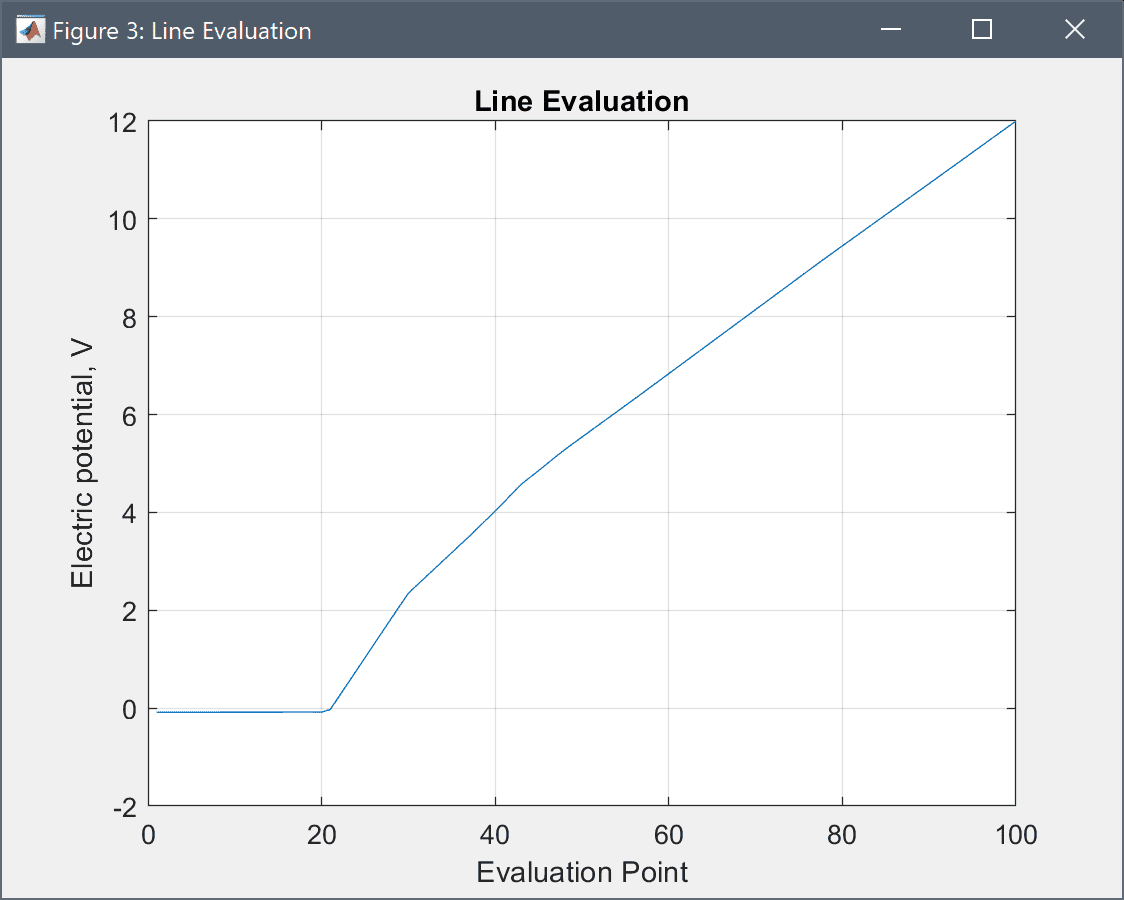
The computed 3D potential is very similar to both the axisymmetric and analytic cases as expected.
V - 24/1e-2*(z-1e-3^3/z^2)*(z>1e-3) into the edit field.The computed errors also show good agreement but could be improved with a finer grid and a higher order approximation.
The conducting sphere electromagnetics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file, or GUI script (.fes) file.
To visualize the full 3D solution from the axisymmetic model, the data can be exported and processed on the MATLAB command line interface (CLI) console with the Export Model Data Struct to MATLAB option from the File menu. The postrevolve and postplot functions can then be applied to revolve and visualize the data, for example
fea_revolved = postrevolve( fea, 24, 0.6 );
% Note that the r-coordinate is replaced by
% "x" in the revolved 3D fea data struct
postplot( fea_revolved, 'surfexpr', 'sqrt(Vx^2+Vz^2)', ...
'parent', figure, 'axis', 'off', 'colorbar', 'off' )
view(0, 25)