
|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|
A shielded electrical microstrip transmission line is fixed to a substrate and placed in a shielded container of air. The simulation applies a known voltage to the strip to calculate the resulting capacitance and compares this with the theoretical result. The problem assumes symmetry in the lengthwise direction so that the model can be reduced to a 2D planar cross-section. The strip is represented by an internal boundary to which the voltage is applied.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Electromagnetics > Microstrip Transmission Line from the File menu. Or alternatively, follow the step-by-step instructions below.
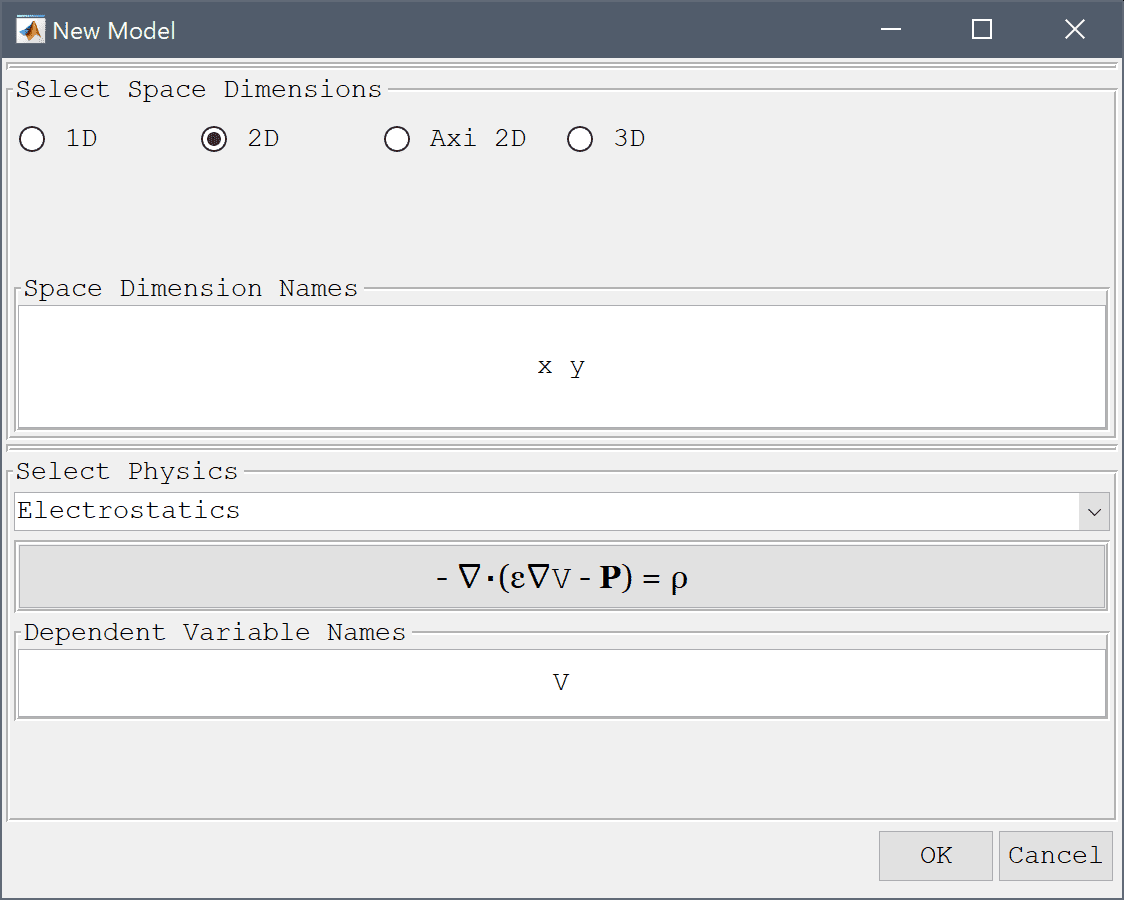
Select the Electrostatics physics mode from the Select Physics drop-down menu.
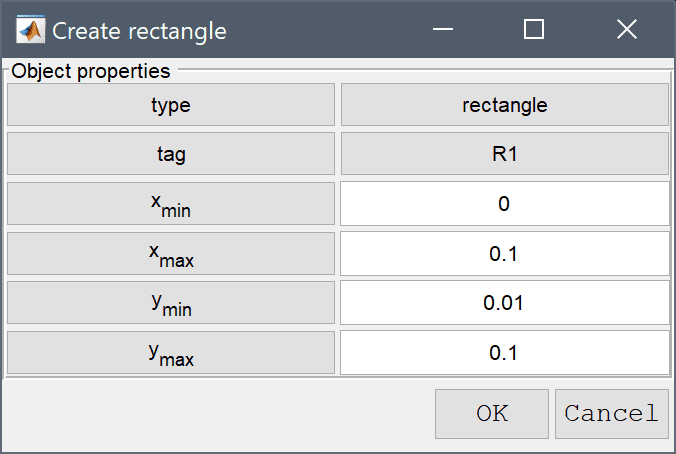
The geometry consists of a 0.1 x 0.09 m rectangle, representing the air, above a 0.1 x 0.01 m rectangle for the substrate.
0.1 and height 0.09 and lower left corner at the origin (0, 0). Finish editing the geometry object and close the dialog box by clicking OK.0 into the xmin edit field.0.1 into the xmax edit field.0.01 into the ymin edit field.Enter 0.1 into the ymax edit field.
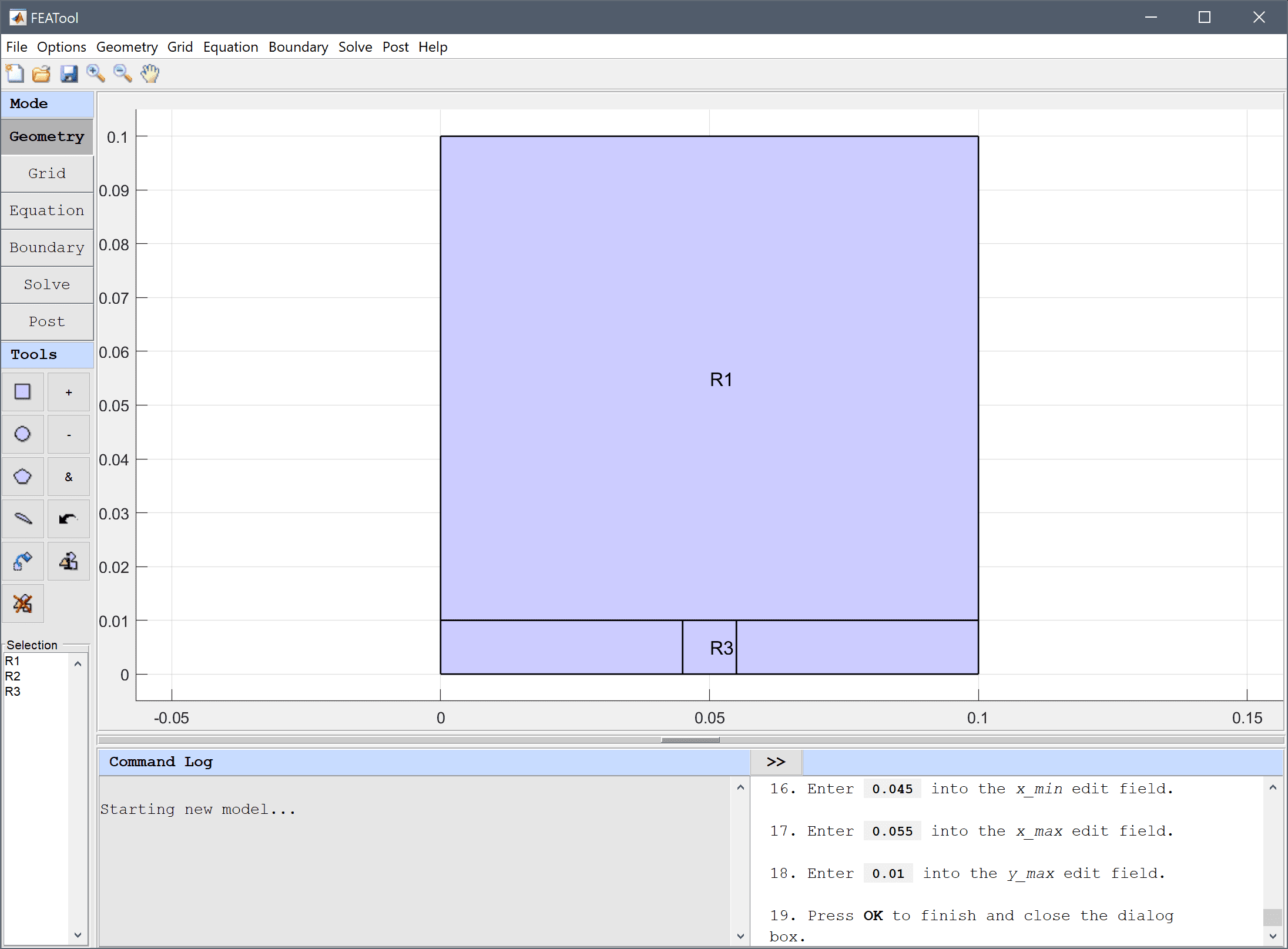
0.1 into the xmax edit field.0.01 into the ymax edit field.To represent the microstrip a 0.01 m interior border is required, to ensure this a third rectangle is created to split the substrate along the microstrip.
0.045 into the xmin edit field.0.055 into the xmax edit field.0.01 into the ymax edit field.Press OK to finish and close the dialog box.
The default grid may be too coarse to ensure an accurate solution. Decrease the target subdomain grid size to 0.001 and press the Generate button to call the automatic grid generation algorithm.
0.001 into the Grid Size edit field.Press the Generate button to call the grid generation algorithm.
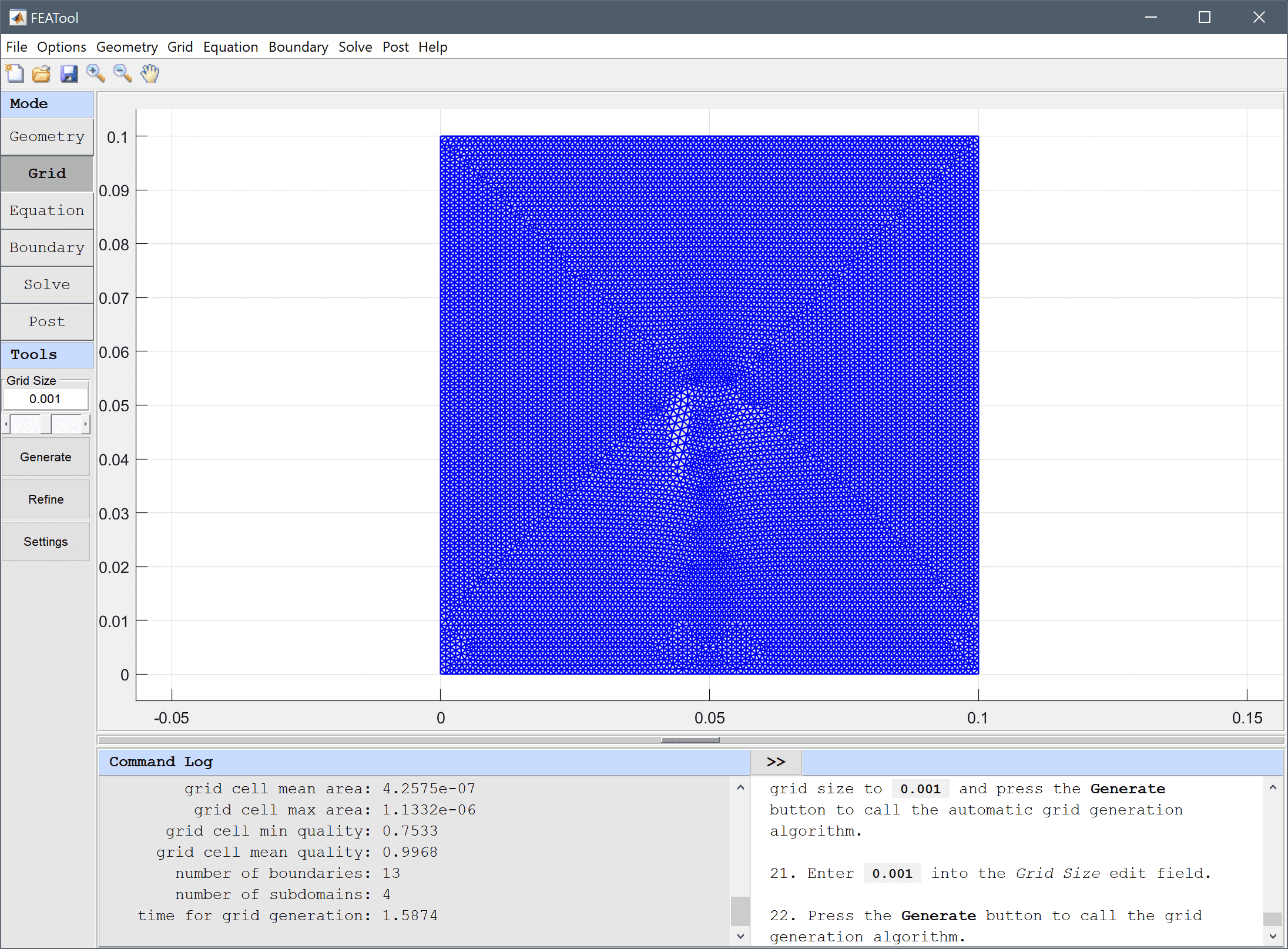
Equation and material coefficients can be specified in Equation/Subdomain mode. In the Equation Settings dialog box that automatically opens, enter the permittivities εrε0, with the relative permittivity εr equal to 1 and 10 in the air and substrate, respectively. The other coefficients can be left to their default values.
1*8.854187817e-12 into the Permittivity edit field.10*8.854187817e-12 into the Permittivity edit field.As the final quantities to compute involve derivatives of the potential a higher order solution space will enable higher accuracy.
Select (P2/Q2) second order conforming from the FEM Discretization drop-down menu.
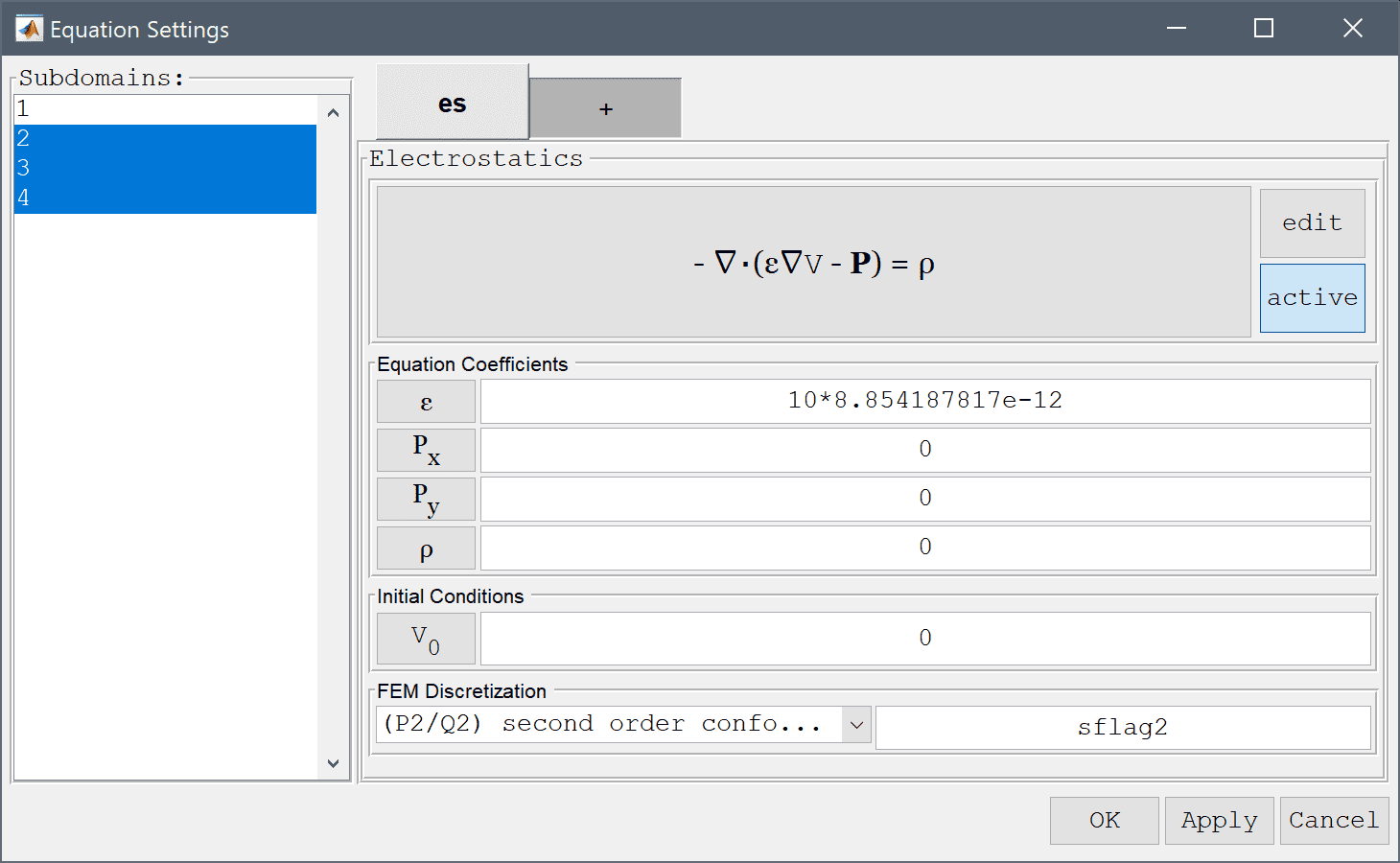
Boundary conditions are defined in Boundary Mode and describes how the model interacts with the external environment. The external boundaries (1-8) represent the shield and should be connected to the ground with zero potential.
Select Ground/antisymmetry from the Electrostatics drop-down menu.
Enter 1 into the Surface charge edit field.
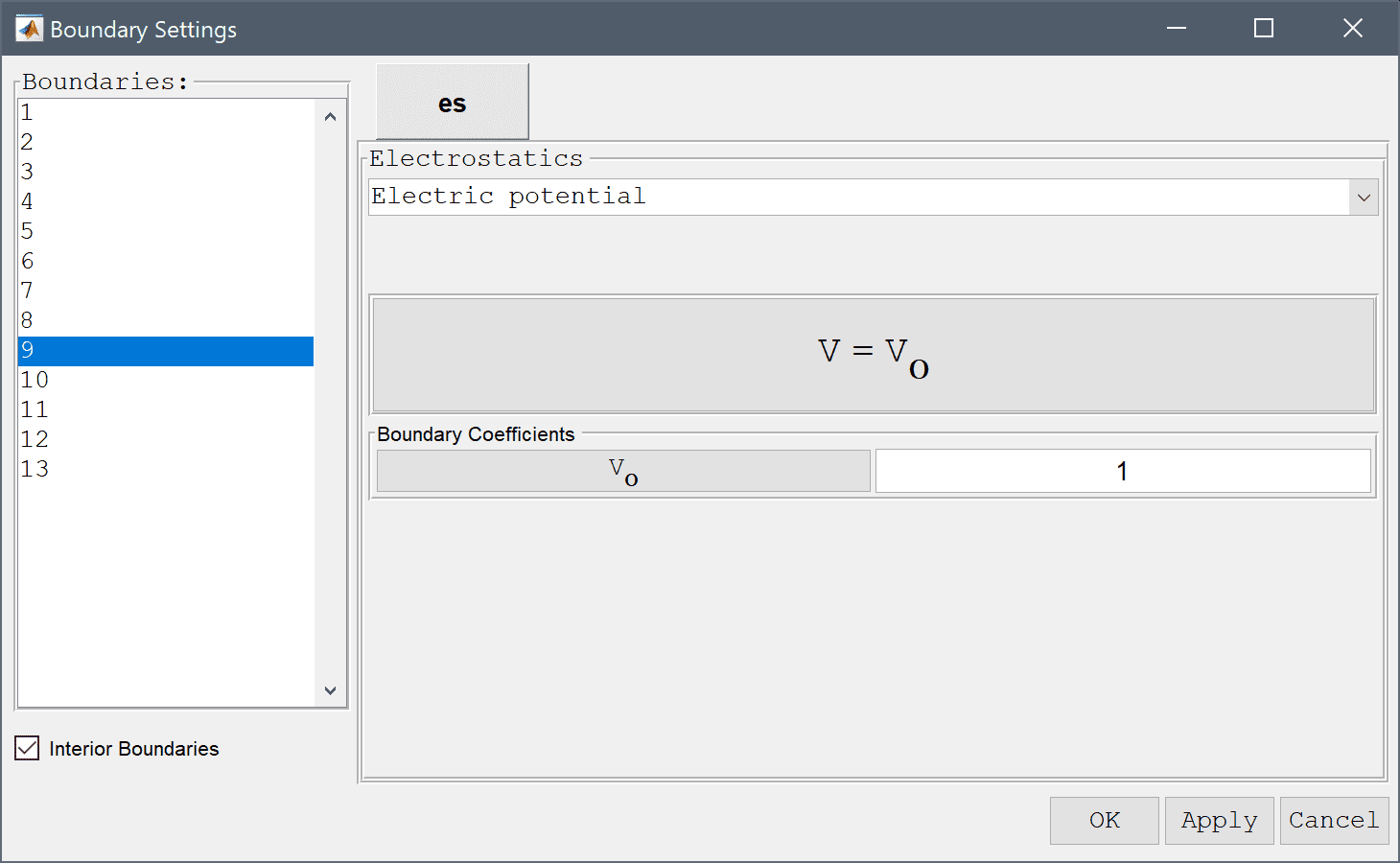
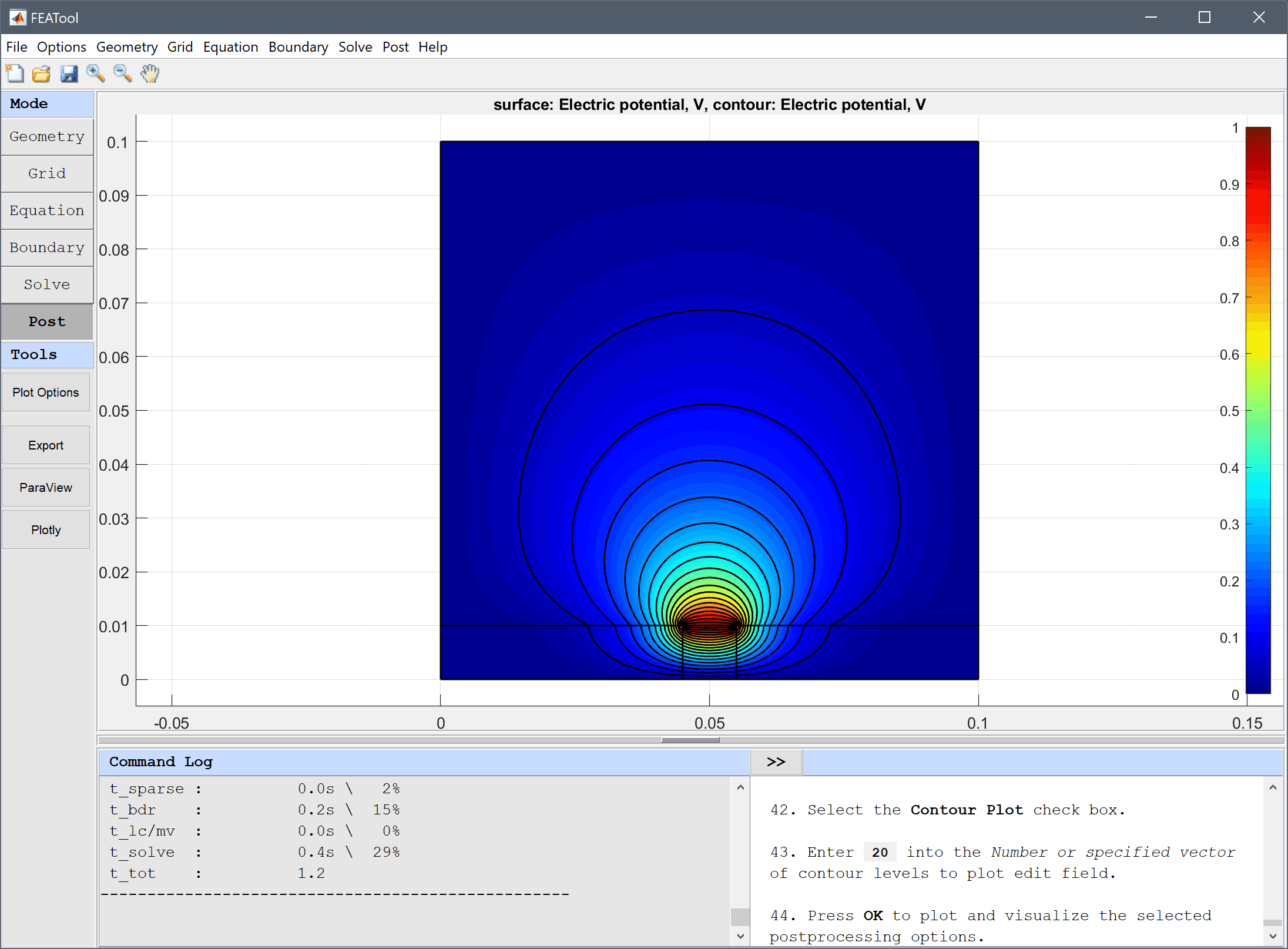
Enter 20 into the Number or specified vector of contour levels to plot edit field.
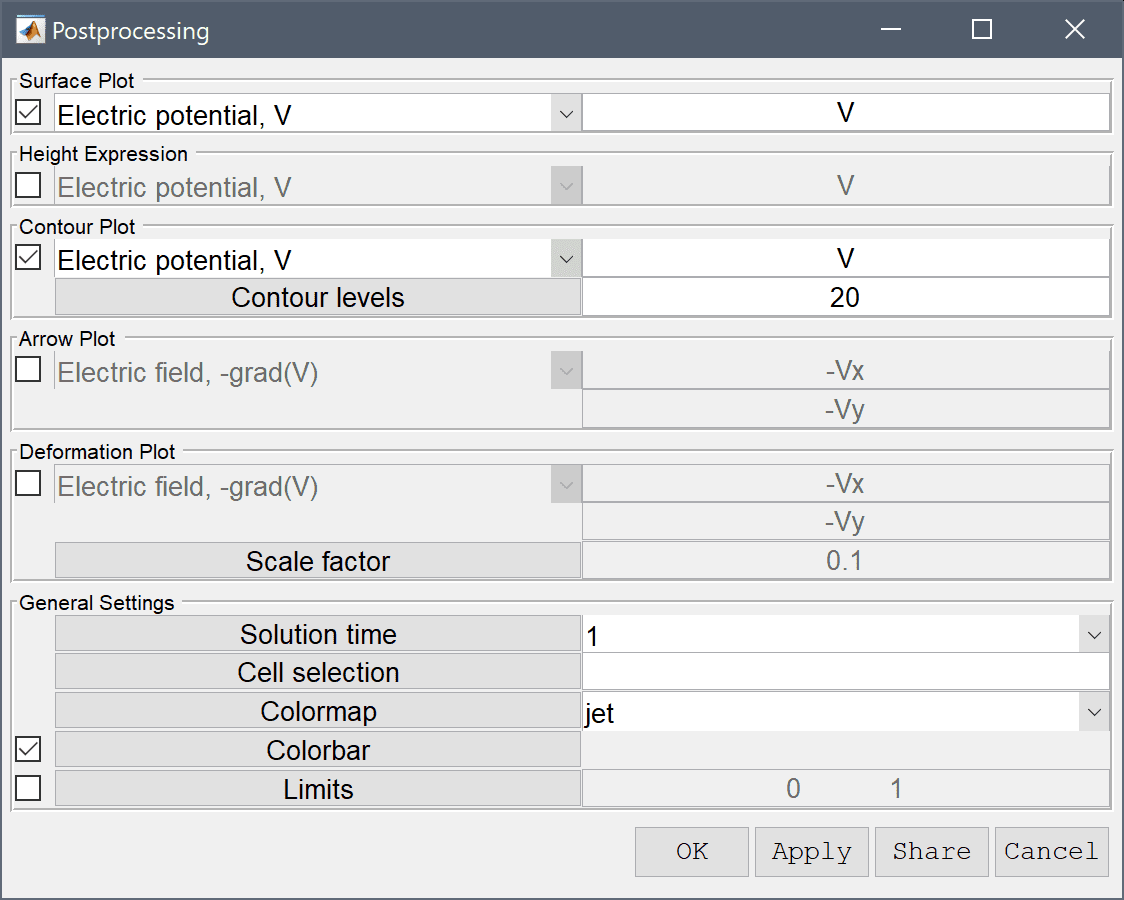
Press OK to plot and visualize the selected postprocessing options.

To validate the solution we will compute the capacitance with two approaches and compare with the theoretical result of C = 178.1 pF.
The first approach is to calculate the total stored energy of the electric field W, and as the voltage U is known, then the capacitance follows as C = 2W/U2.
Modify the expression to account for the energy factor 2 and division by the voltage squared.
2*( 0.5*((-eps_es*Vx+Px_es)*(-Vx)+(-eps_es*Vy+Py_es)*(-Vy)) )/1^2 into the Integration Expression edit field.Press the Apply button.
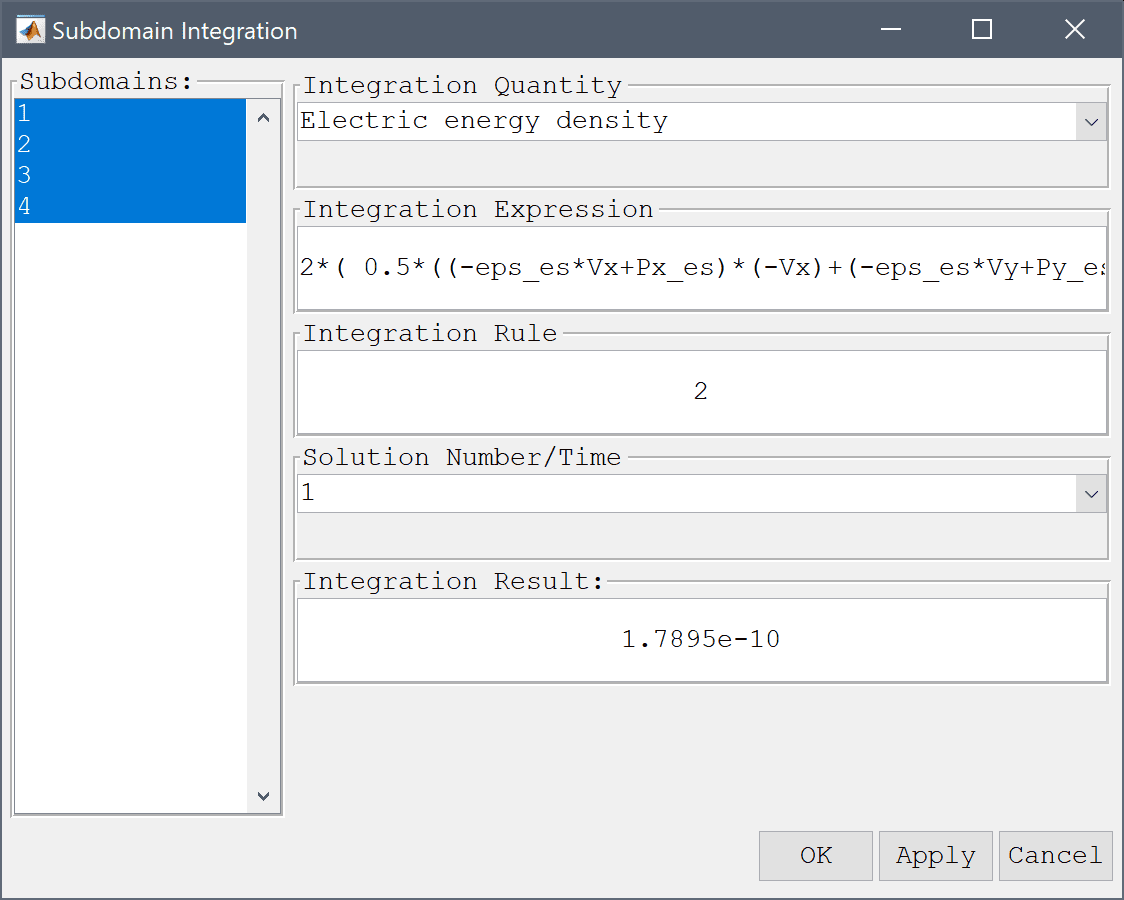
The second approach is to calculate the electric charge around the strip q and divide by the known voltage U.
Modify the expression to account for division by the voltage.
( -nx*(-eps_es*Vx+Px_es)-ny*(-eps_es*Vy+Py_es) )/1 into the Integration Expression edit field.Press the Apply button.
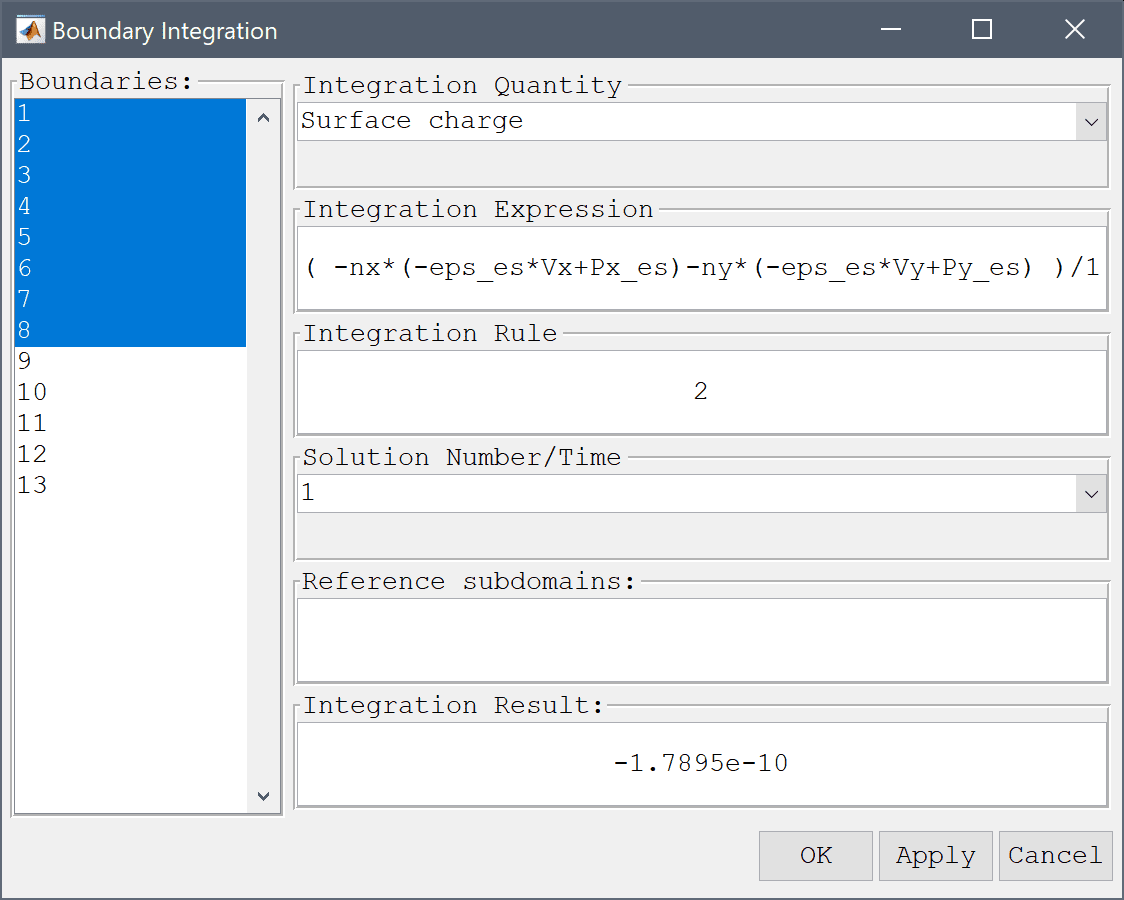
Both approaches should yield results within 0.1 % of the theoretical expected result.
The microstrip transmission line electromagnetics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file, or GUI script (.fes) file.