
|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|
Stationary and laminar incompressible flow in a square cavity (Reynolds number, Re = 1000). The top of the cavity is prescribed a tangential velocity while the sides and bottom are defined as no-slip zero velocity walls.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Fluid Dynamics > Flow in Driven Cavity from the File menu. Or alternatively, follow the step-by-step instructions below.
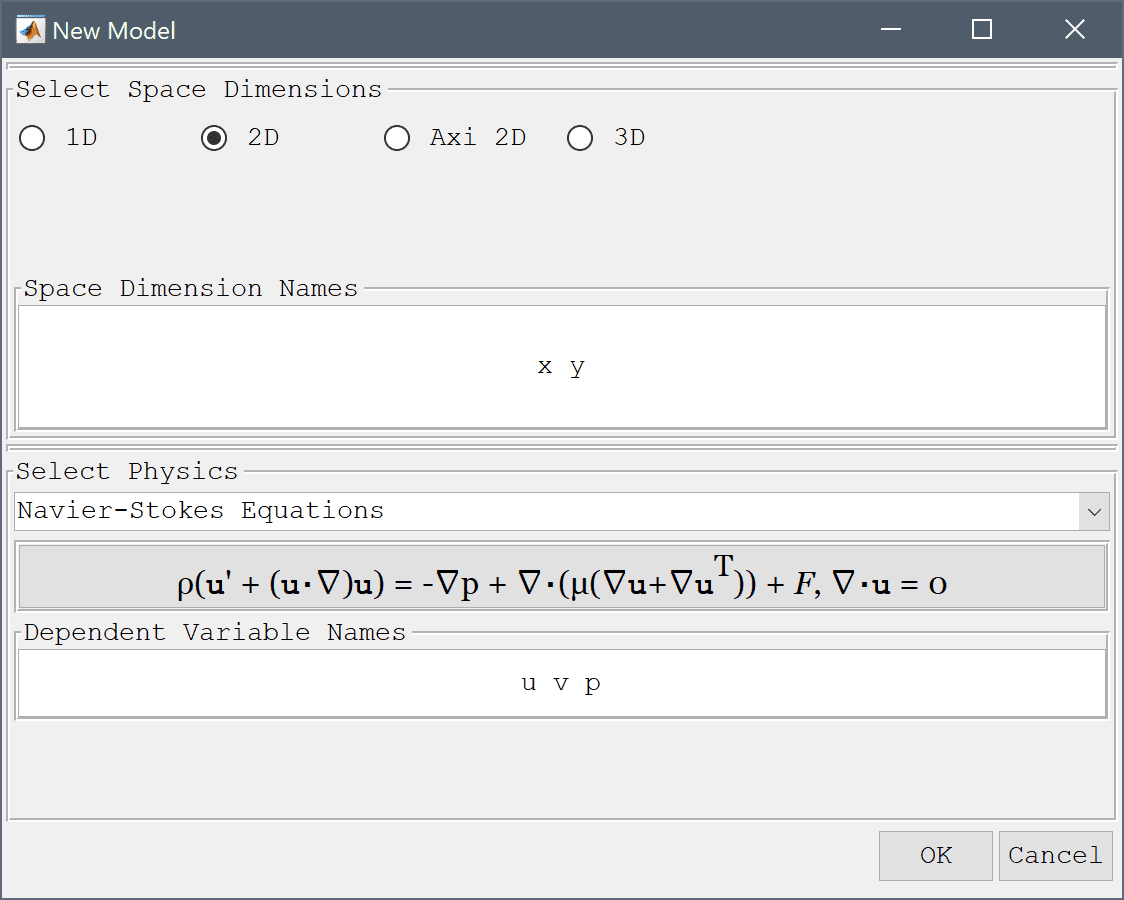
Select the Navier-Stokes Equations physics mode from the Select Physics drop-down menu.
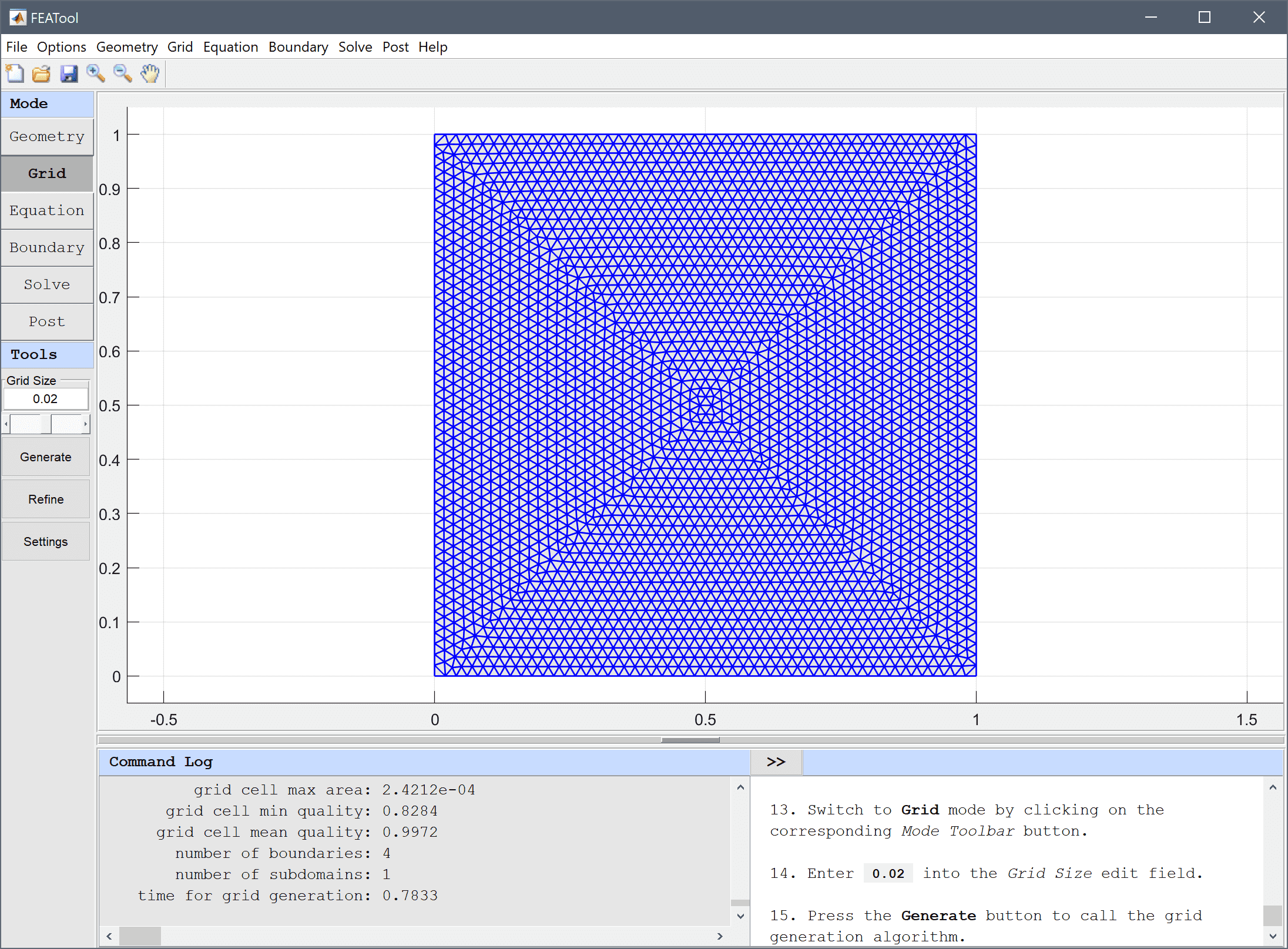
First create a unit square for the geometry.
0 into the xmin edit field.1 into the xmax edit field.0 into the ymin edit field.1 into the ymax edit field.0.02 into the Grid Size edit field.Press the Generate button to call the grid generation algorithm.
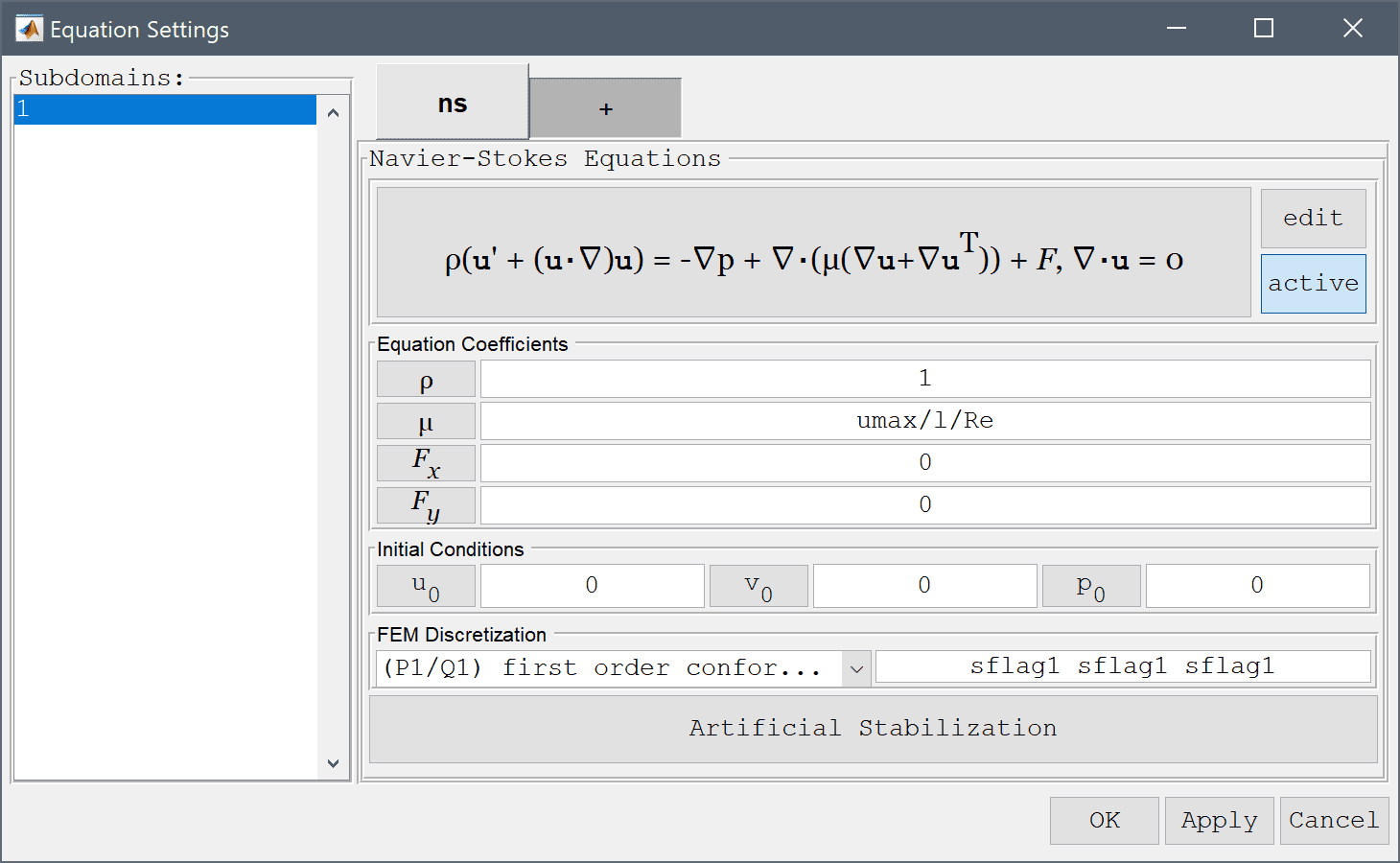
Equation and material coefficients can be specified in Equation/Subdomain mode. In the Equation Settings dialog box that automatically opens, enter 1 for the fluid Density and umax/l/R for the Viscosity. The other coefficients can be left to their default values. Press OK to finish the equation and subdomain settings specification.
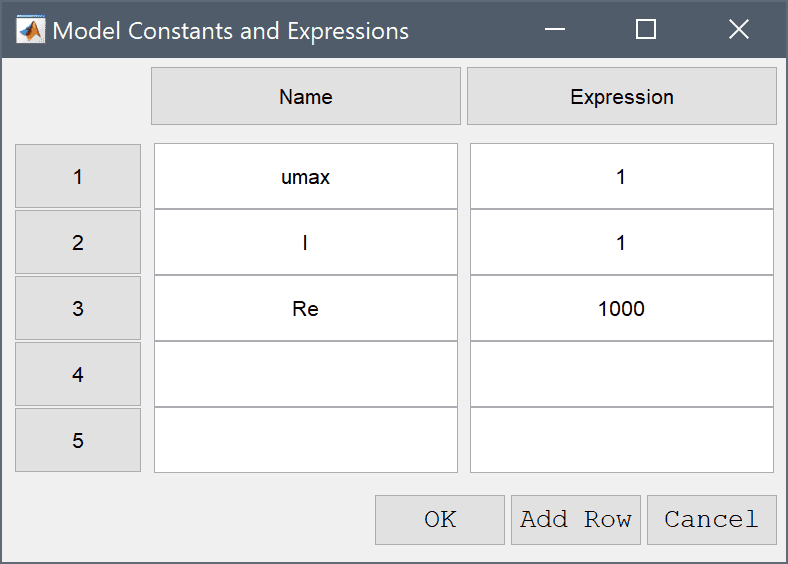
Note that FEATool works with any unit system, and that the units here are non-dimensionalized.
| Name | Expression |
|---|---|
| umax | 1 |
| l | 1 |
| Re | 1000 |
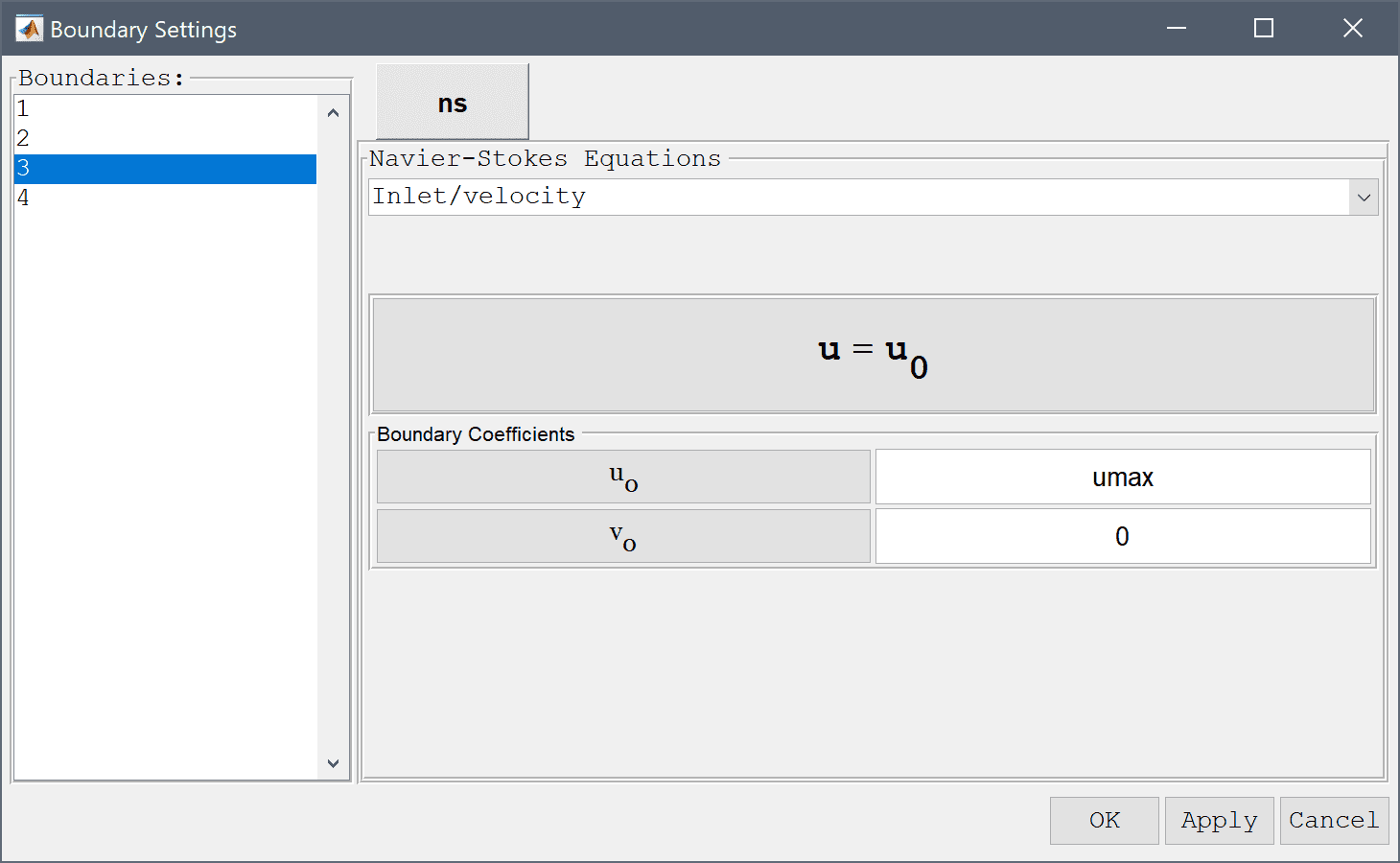
Boundary conditions consist of no-slip zero velocity conditions on all walls except for the top on which a constant x-velocity umax is prescribed.
Enter umax into the Velocity in x-direction edit field.
Now that the problem is fully specified, press the Solve Mode Toolbar button to switch to solve mode. Then press the = Tool button to call the solver with the default solver settings.
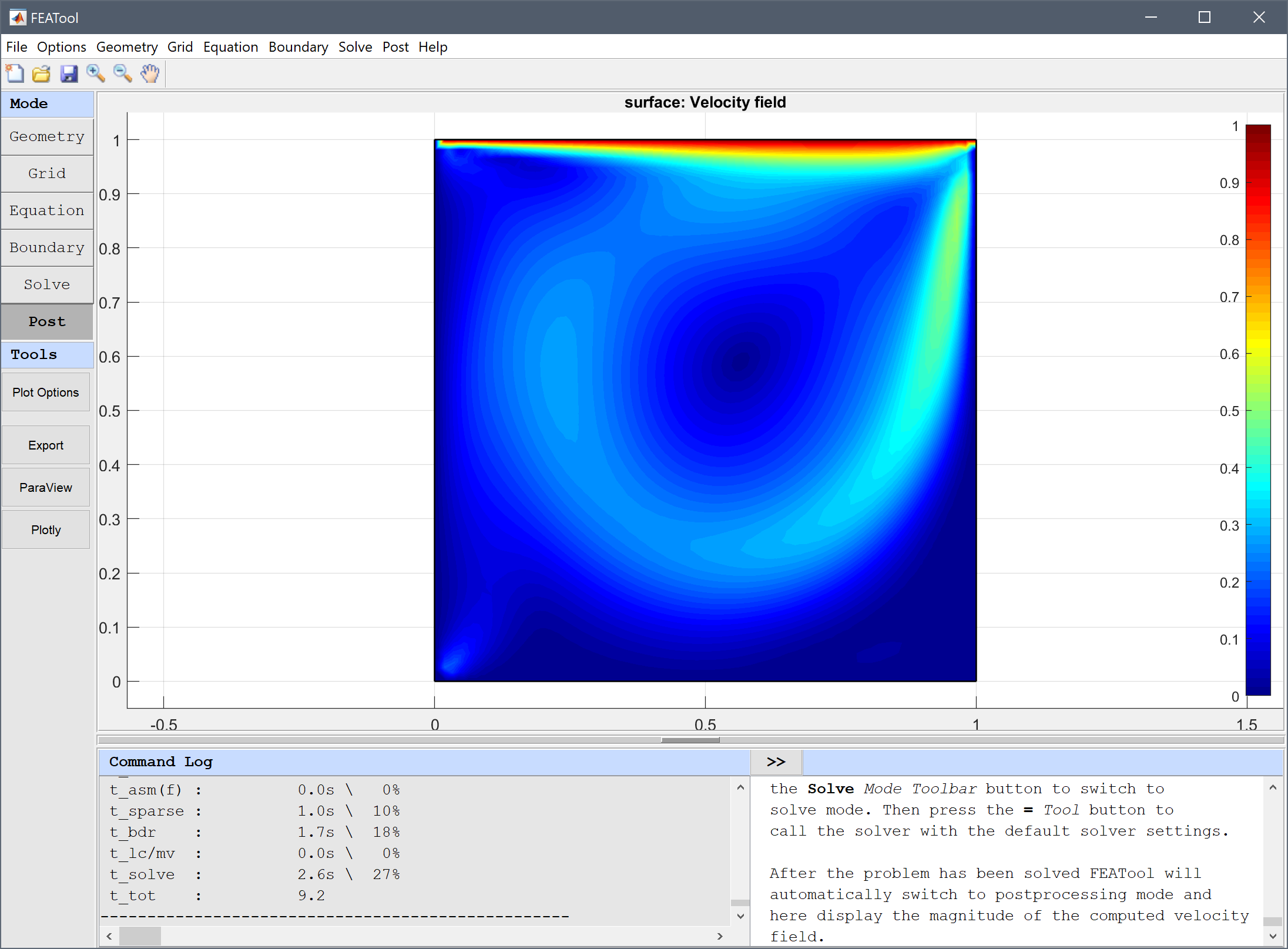
After the problem has been solved FEATool will automatically switch to postprocessing mode and here display the magnitude of the computed velocity field.
30 into the Number or specified vector of contour levels to plot edit field.Press OK to plot and visualize the selected postprocessing options.
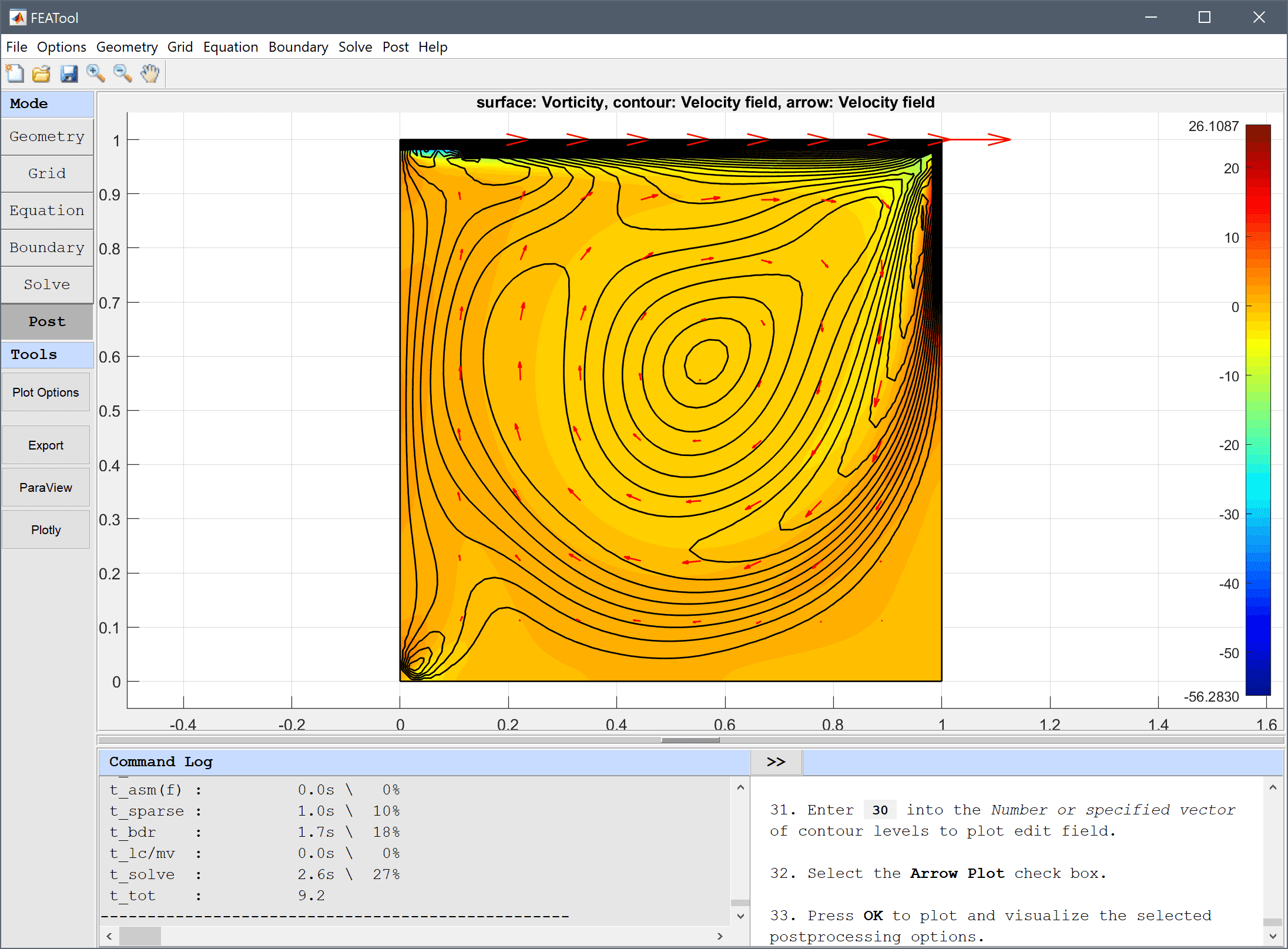
To evaluate the accuracy of the solution the vorticity at (0.53, 0.56) is evaluated. Either click directly at this point or use the Point/Line Evaluation functionality.
0.53 into the Evaluation coordinates in x-direction edit field.Enter 0.564 into the Evaluation coordinates in y-direction edit field.
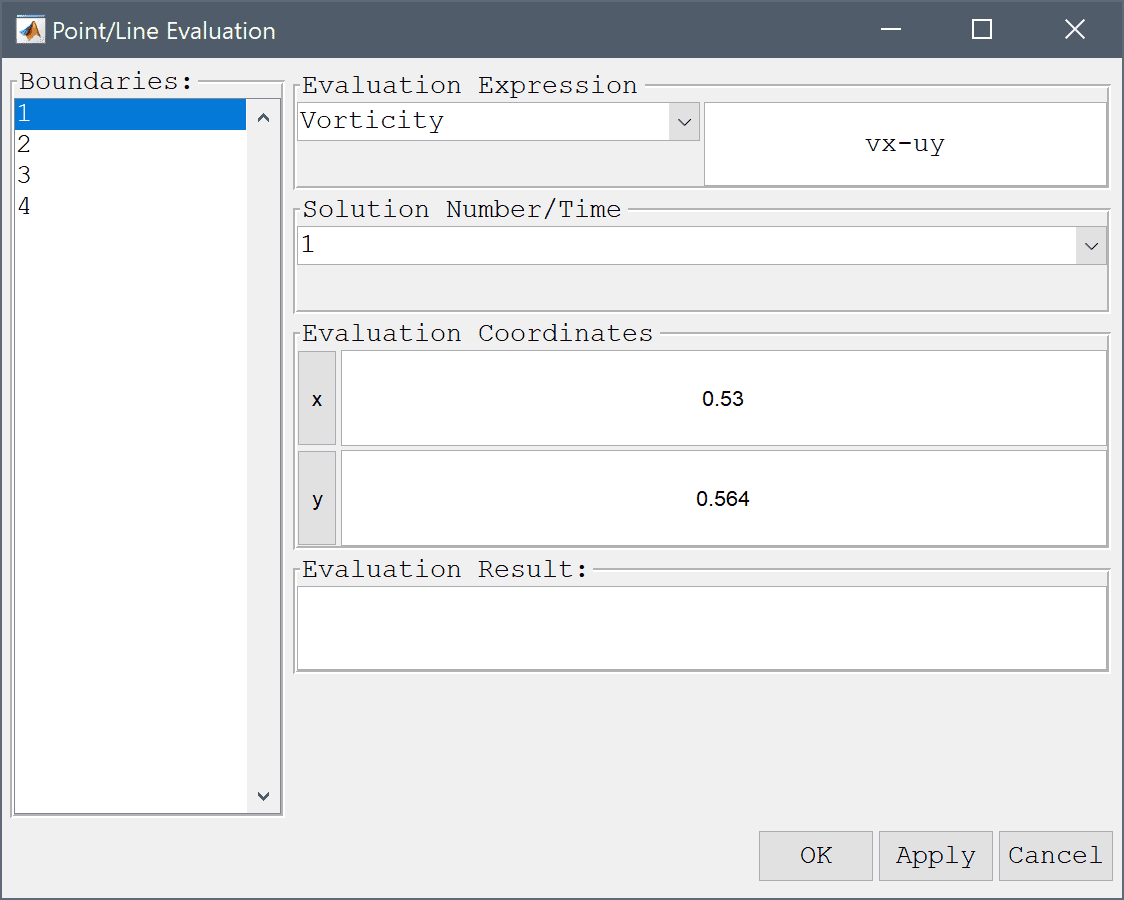
Press OK to finish and close the dialog box.
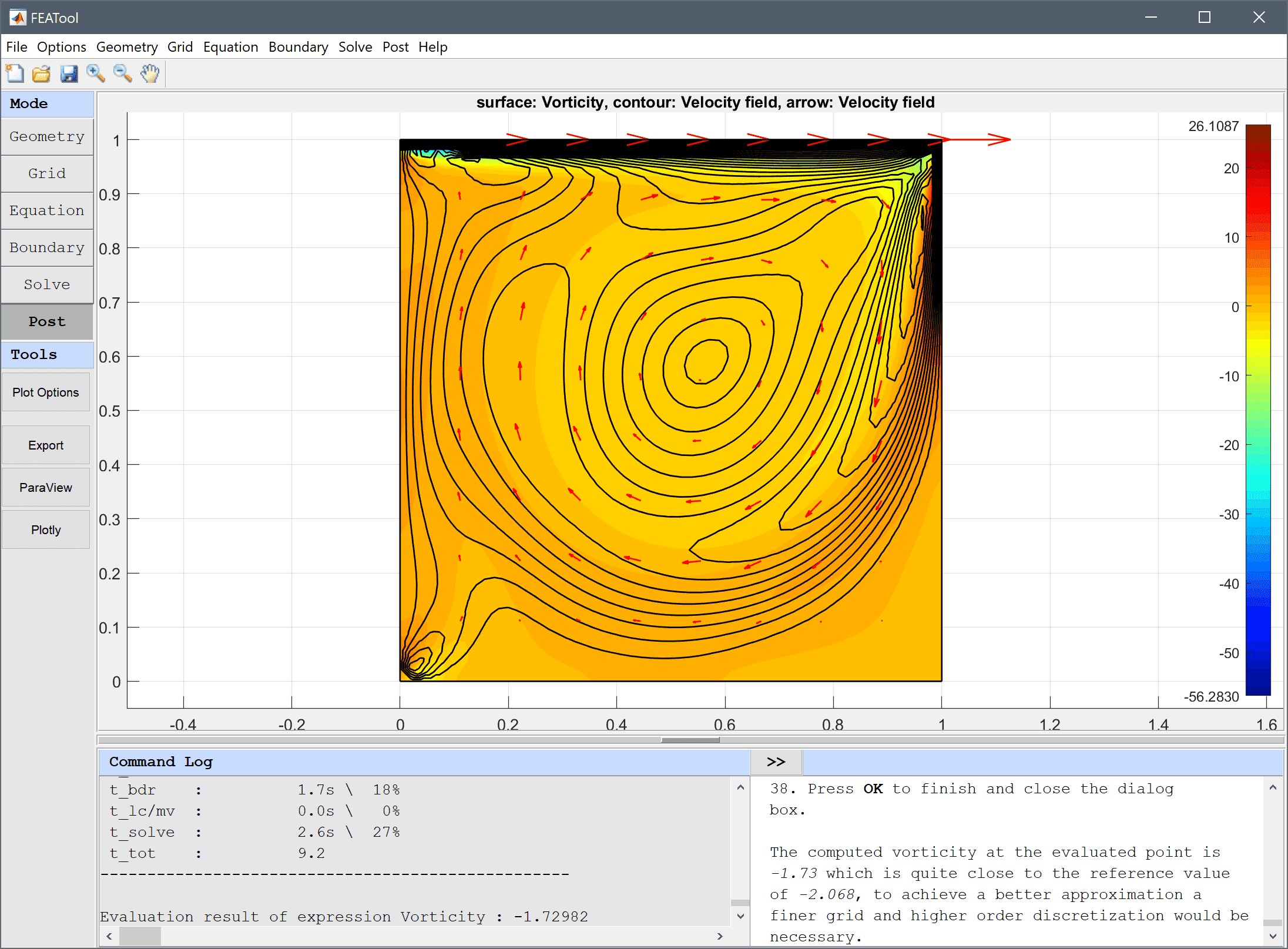
The computed vorticity at the evaluated point is -1.73 which is quite close to the reference value of -2.068, to achieve a better approximation a finer grid and higher order discretization would be necessary.
The flow in driven cavity fluid dynamics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file (available as the example ex_navierstokes2 script file), or GUI script (.fes) file.
[1] Botella O, Peyret R. Benchmark spectral results on the lid-driven cavity flow. Computers and Fluids 27(4):421-433, 1998.
[2] Erturk E, Corke TC, Gokcol C. Numerical solutions of 2-D steady incompressible driven cavity flow at high Reynolds numbers. Int- ernational Journal for Numerical Methods in Fluids 37(6):633-655, 2005.
[3] Nishida H, Satofuka N. Higher-order solutions of square driven cavity flow using a variable-order multi-grid method. International Journal for Numerical Methods in Engineering 34(2):637-653, 1992.
[4] Schreiber R, Keller HB. Driven cavity flows by efficient numerical techniques. Journal of Computational Physics 49(2):310-333, 1983.