
|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|
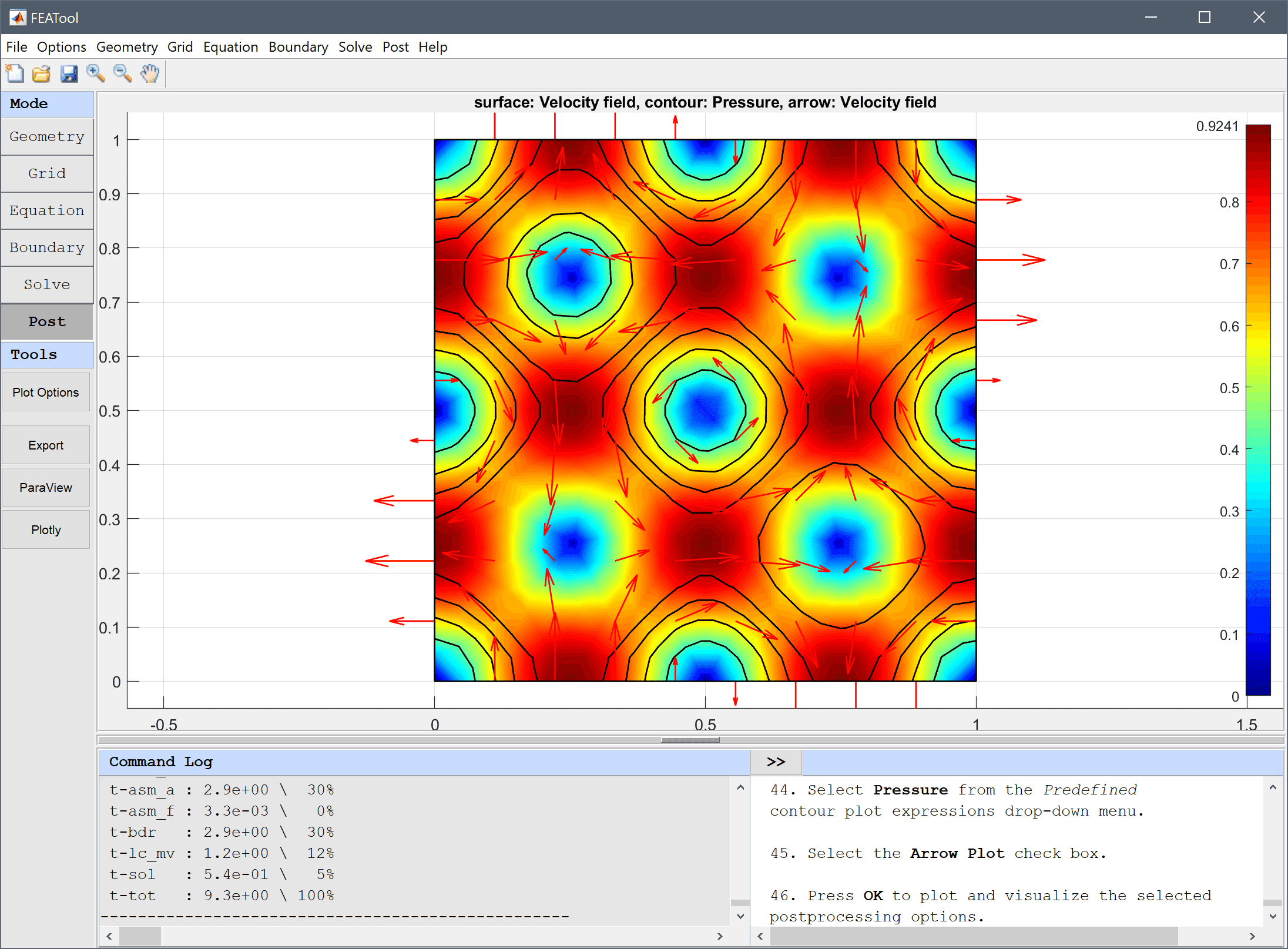
Time dependent decaying flow for standing vortices with the following analytical solution to the Navier-Stokes equations
\[ \left\{\begin{array}{l} u = -cos(kx) sin(ky) e^{-2\nu k^2t} \\ v = sin(kx) cos(ky) e^{-2\nu k^2 t} \\ p = -\frac{1}{4}(cos(2kx)+cos(2ky)) e^{-4\nu k^2 t} \end{array}\right. \]
The two-dimensional flow problem is solved for a unit square with k = 2π and the exact solution as boundary and initial conditions.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Fluid Dynamics > Vortex Flow from the File menu. Or alternatively, follow the step-by-step instructions below.
0 into the xmin edit field.1 into the xmax edit field.0 into the ymin edit field.1 into the ymax edit field.0.05 into the Grid Size edit field.| Name | Expression |
|---|---|
| nu | 0.0.1 |
| k | 2*pi |
| u_ref | -cos(k*x)*sin(k*y)*exp(-2*nu*k^2*t) |
| v_ref | sin(k*x)*cos(k*y)*exp(-2*nu*k^2*t) |
| p_ref | -1/4*(cos(2*k*x)+cos(2*k*y))*exp(-4*nu*k^2*t) |
Open the Equation Settings dialog box and enter nu for the viscosity and the reference expressions as initial conditions
nu into the Viscosity edit field.u_ref into the Initial condition for u edit field.v_ref into the Initial condition for v edit field.p_ref into the Initial condition for p edit field.Prescribe the reference velocities on all boundaries using the Inlet/velocity boundary condition.
u_ref into the Velocity in x-direction edit field.v_ref into the Velocity in y-direction edit field.Also prescribe the reference pressure on all four points. Note that since no outflow is present in this model, a reference point with pressure p_ref = 0 has already been prescribed. This is necessary to ensure convergence and a unique pressure for stationary problems without any outflow boundary conditions.
p_ref into the corresponding edit field for the pressure constraint expression. Press OK to finish and close the dialog box.0.01 into the Time step size edit field.0.1 into the Duration of time-dependent simulation (maximum time) edit field.Plot the velocity field as arrows and pressure as contour plot to see the vortices of the flow field.
By plotting and visualizing the difference between the computed and reference variables, the overall accuracy of the simulation can be estimated.
u-u_ref into the User defined surface plot expression edit field.The vortex flow fluid dynamics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file (available as the example ex_navierstokes5 script file), or GUI script (.fes) file.