
|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|
Simulation of stationary and incompressible turbulent flow between two parallel flat plates at Reynolds number 42800. A fully developed turbulent velocity profile is formed at the outflow boundary which can be compared to experimental results (Laufer, J. 1950).
This example uses both the built-in algebraic mixing length turbulence model, as well as shows how to implement custom user-defined modeling expressions.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Fluid Dynamics > Turbulent Channel Flow from the File menu. Or alternatively, follow the step-by-step instructions below.
Select the Navier-Stokes Equations physics mode from the Select Physics drop-down menu.
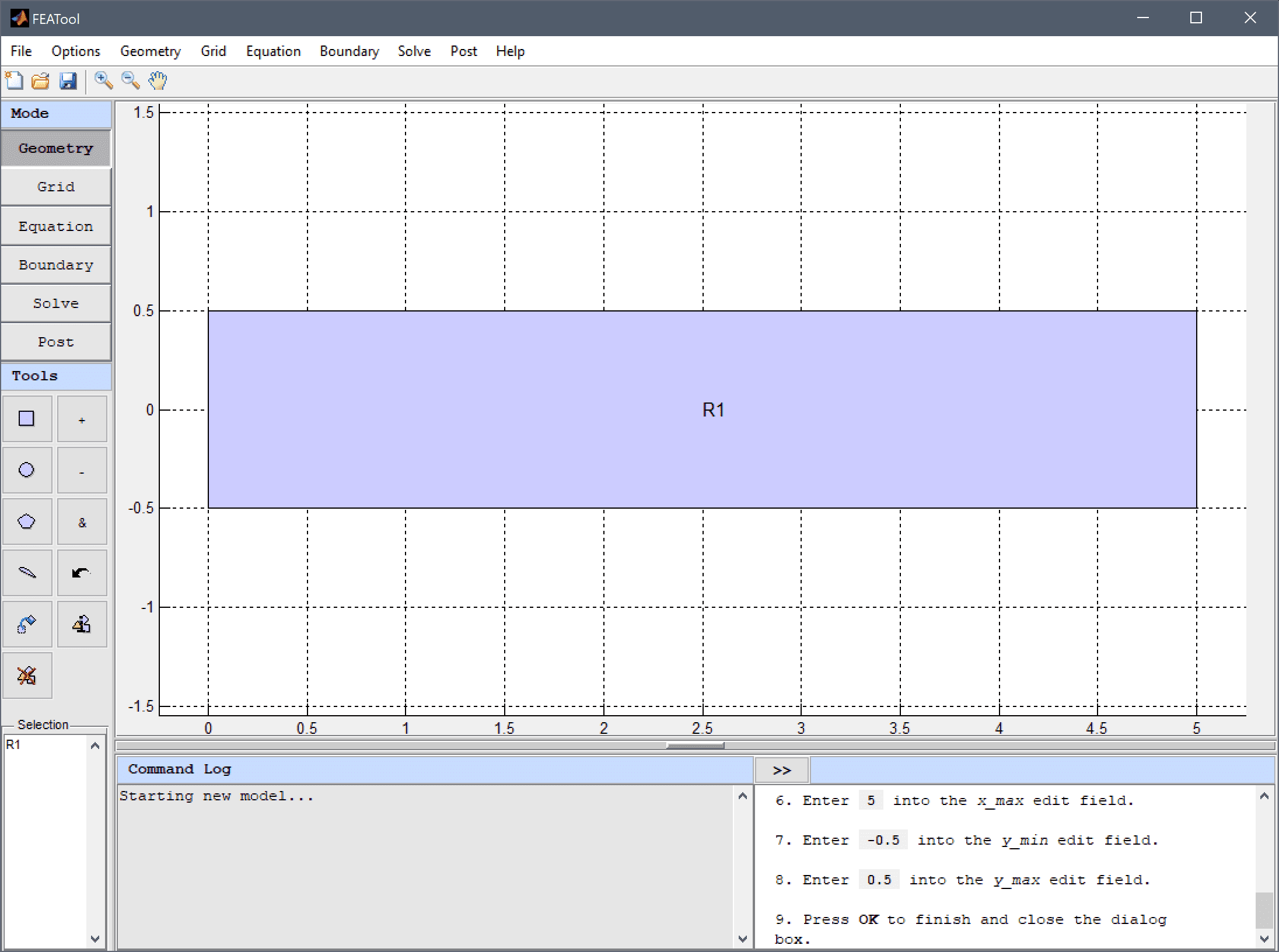
The first step is to create a 1 by 5 rectangle to represent the fluid domain.
0 into the xmin edit field.5 into the xmax edit field.-0.5 into the ymin edit field.0.5 into the ymax edit field.Press OK to finish and close the dialog box.
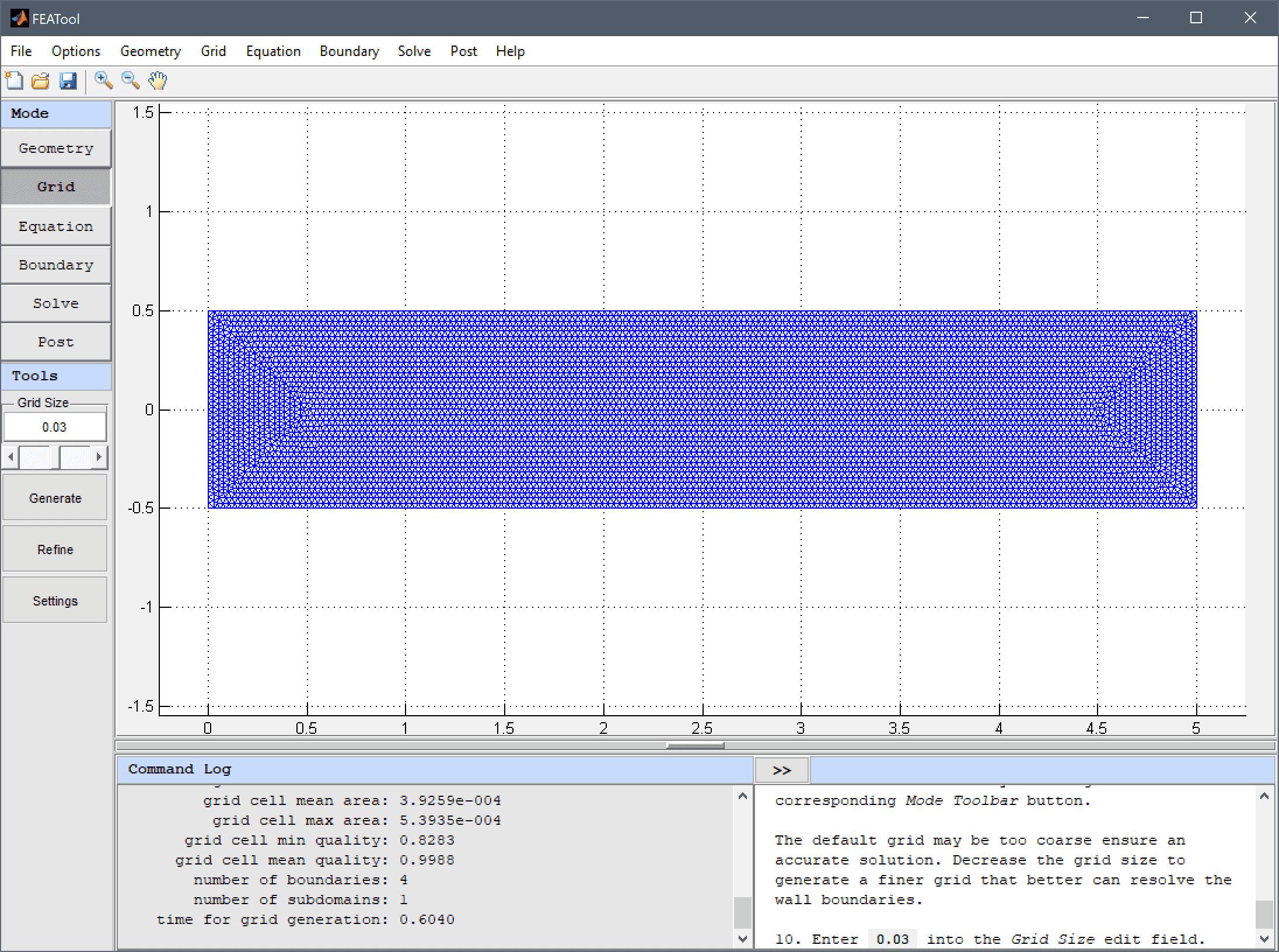
The default grid may be too coarse to ensure an accurate solution. Decrease the grid size to generate a finer grid that better can resolve the wall boundaries which are expected to feature sharp flow gradients.
Enter 0.03 into the Grid Size edit field and press the Generate button to call the automatic grid generation algorithm.
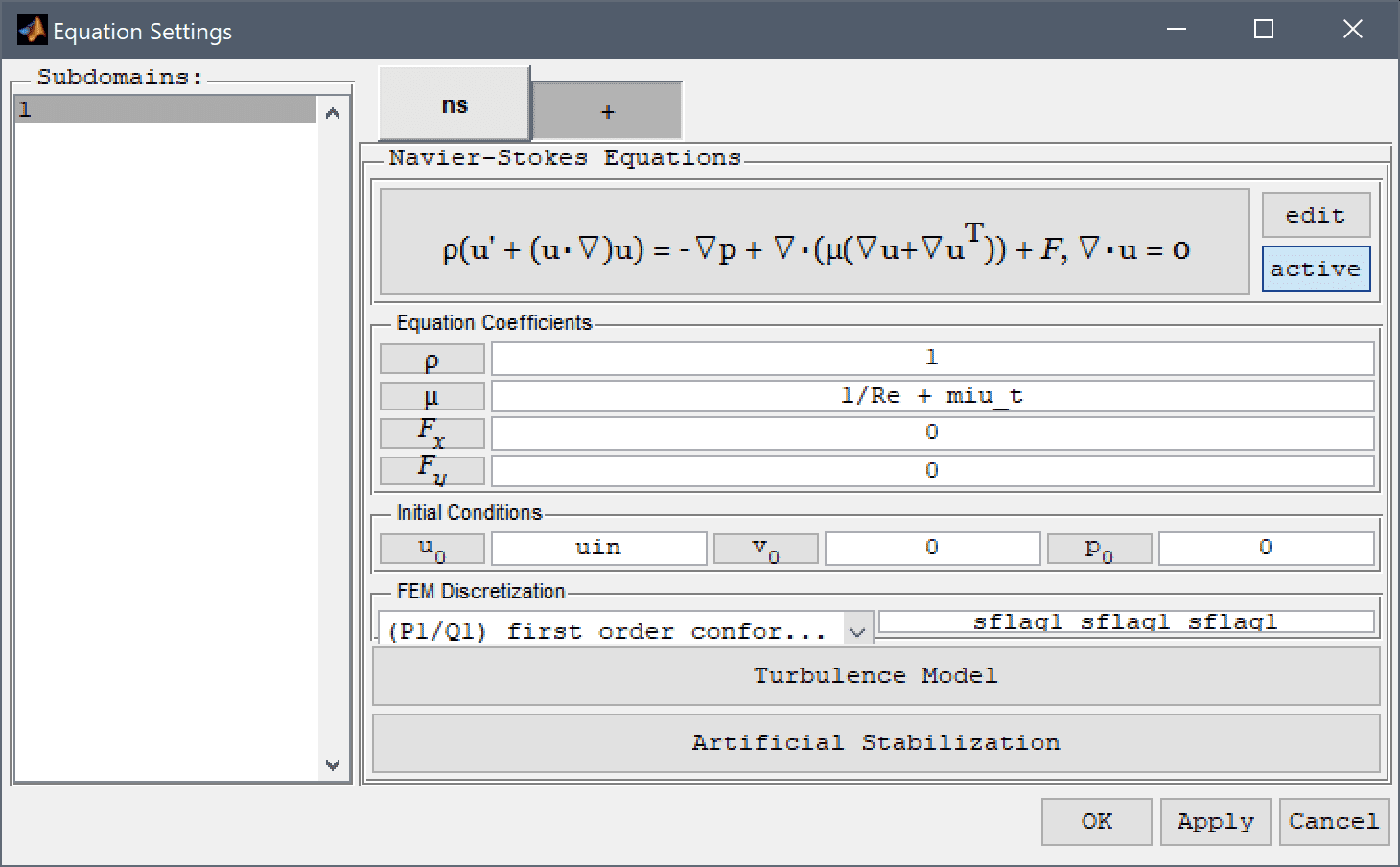
Equation and material coefficients are specified in Equation/Subdomain mode. In the Equation Settings dialog box that automatically opens when switching to Equation mode, enter 1 for the fluid Density, 1/Re for the Viscosity, and uin for the initial velocity in the x-direction u0.
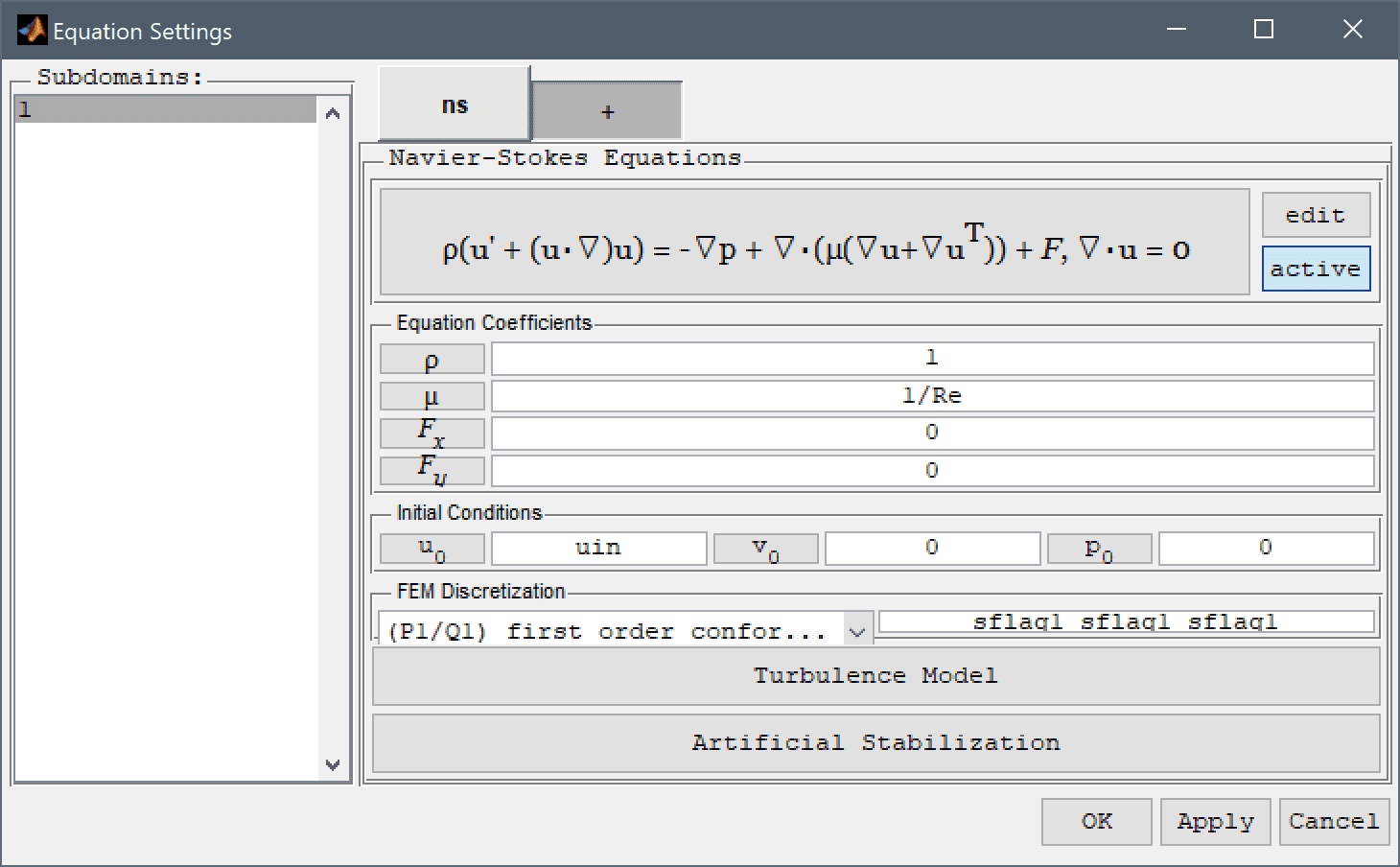
Note that FEATool works with any unit system, and in this model non-dimensionalized units are used. It is up to the user to use consistent units for geometry dimensions, material, equation, and boundary coefficients.
Press the Turbulence Model button and select the Algebraic (mixing length model). The algebraic mixing length model is available with the built-in solvers while the more advanced k-epsilon and omega turbulence models requires using the external OpenFOAM CFD solver.
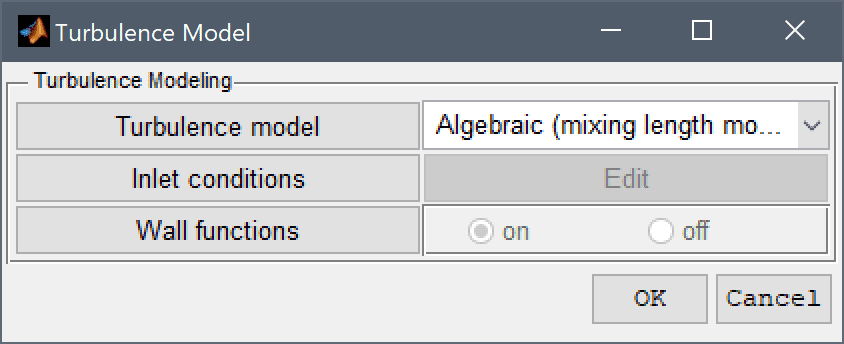
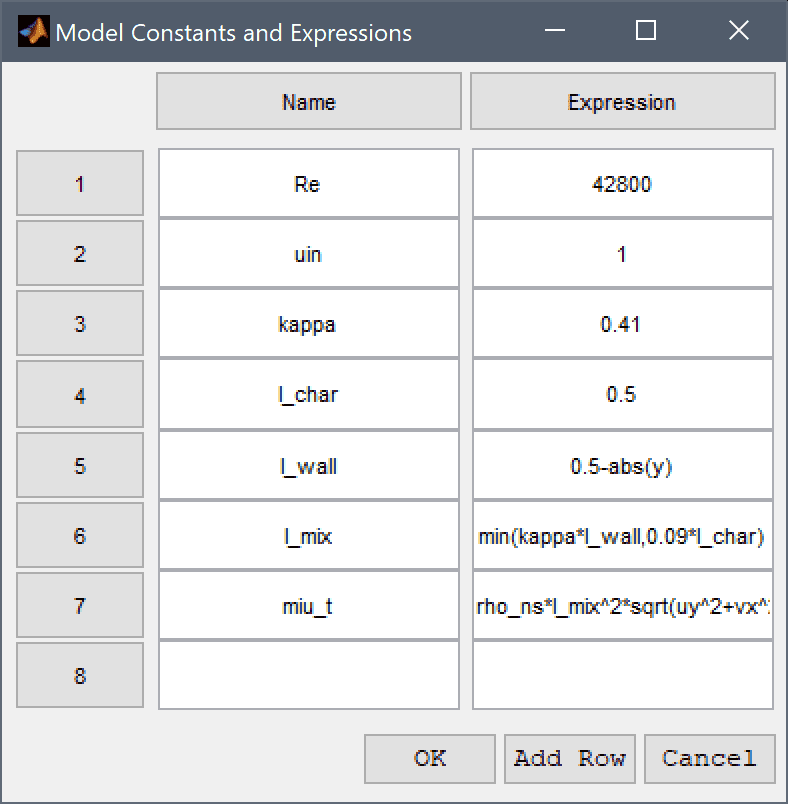
A convenient way to define and store coefficients, variables, and expressions is to use the Model Constants and Expressions functionality. The defined expressions can then be used in point, equation, boundary coefficients, as well as postprocessing expressions, and can easily be changed and updated in a single place.
Enter the expressions for the Reynolds number, Re = 42800 which reciprocal is used to define the viscosity, and inlet velocity, uin = 1 used in both the initial and boundary conditions.
Boundary conditions are defined in Boundary mode and describes how the model interacts with the external environment. Switch to Boundary mode by clicking on the corresponding button.
First select (no-slip) walls for the top and bottom boundaries.
The fluid flows from left to right, so select an outflow condition for the right boundary.
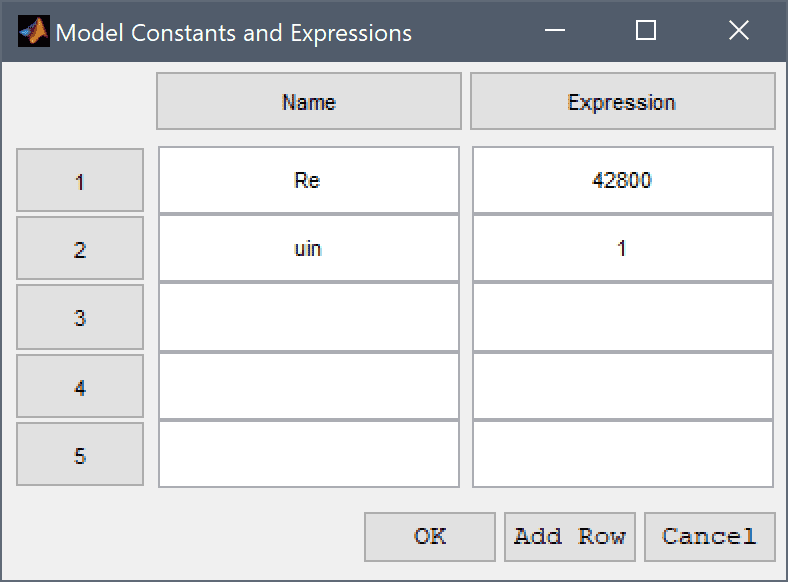
Finally, set the left boundary as an inflow with x-velocity uin.
Enter uin into the Velocity in x-direction edit field.
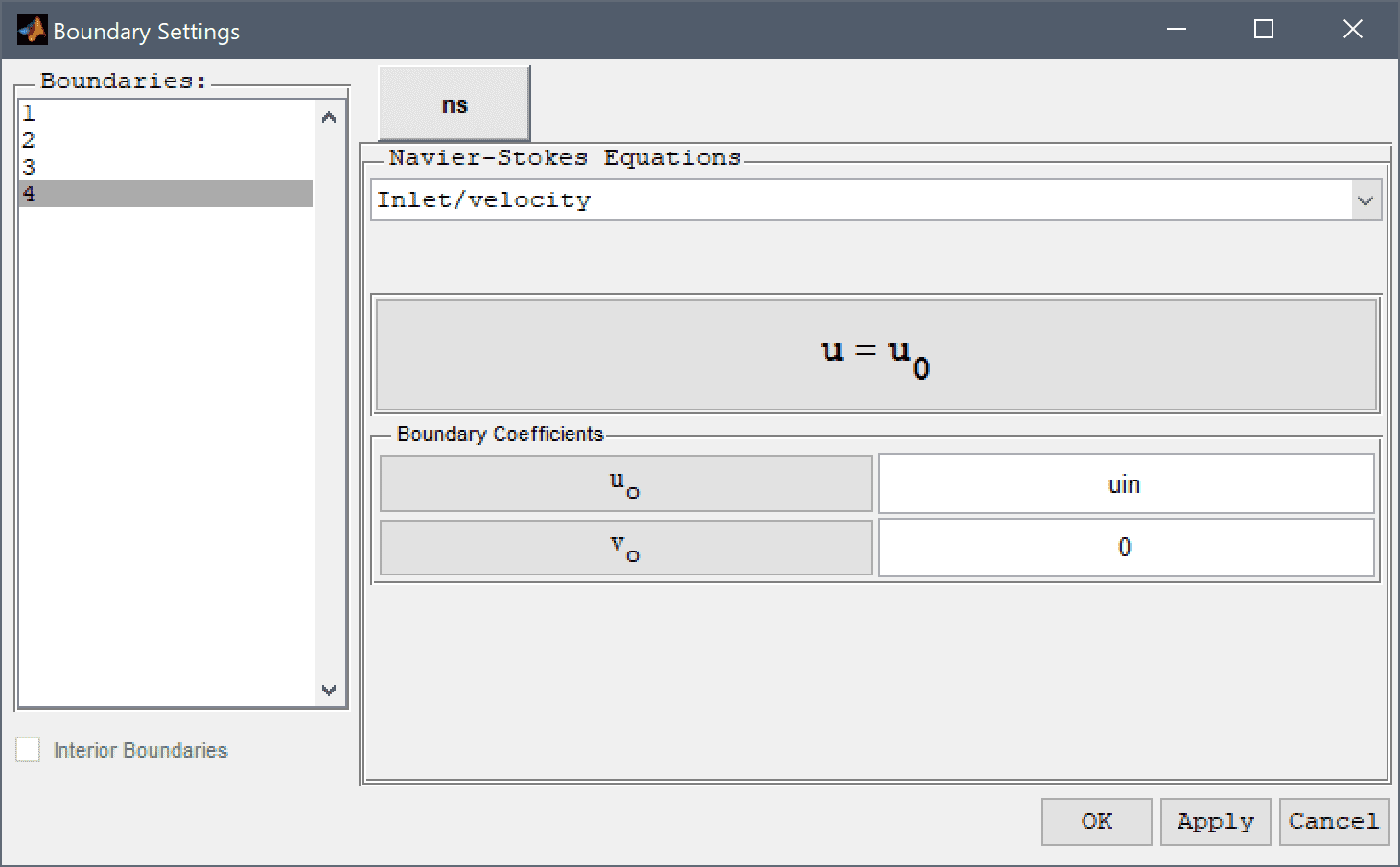
As turbulent flow problems are very non-linear, decrease the non-linear relaxation and tolerances to in the Solver Settings dialog box to help with convergence.
0.5 into the Non-linear relaxation parameter (ratio of new to old solution to use) edit field.1e-3 into the Non-linear stopping criteria for solution defects edit field.Enter 1e-4 into the Non-linear stopping criteria for solution differences (changes) between iterations edit field.
After the problem has been solved FEATool will automatically switch to postprocessing mode and here display the magnitude of the computed velocity field.
Select the Contour Plot check box.
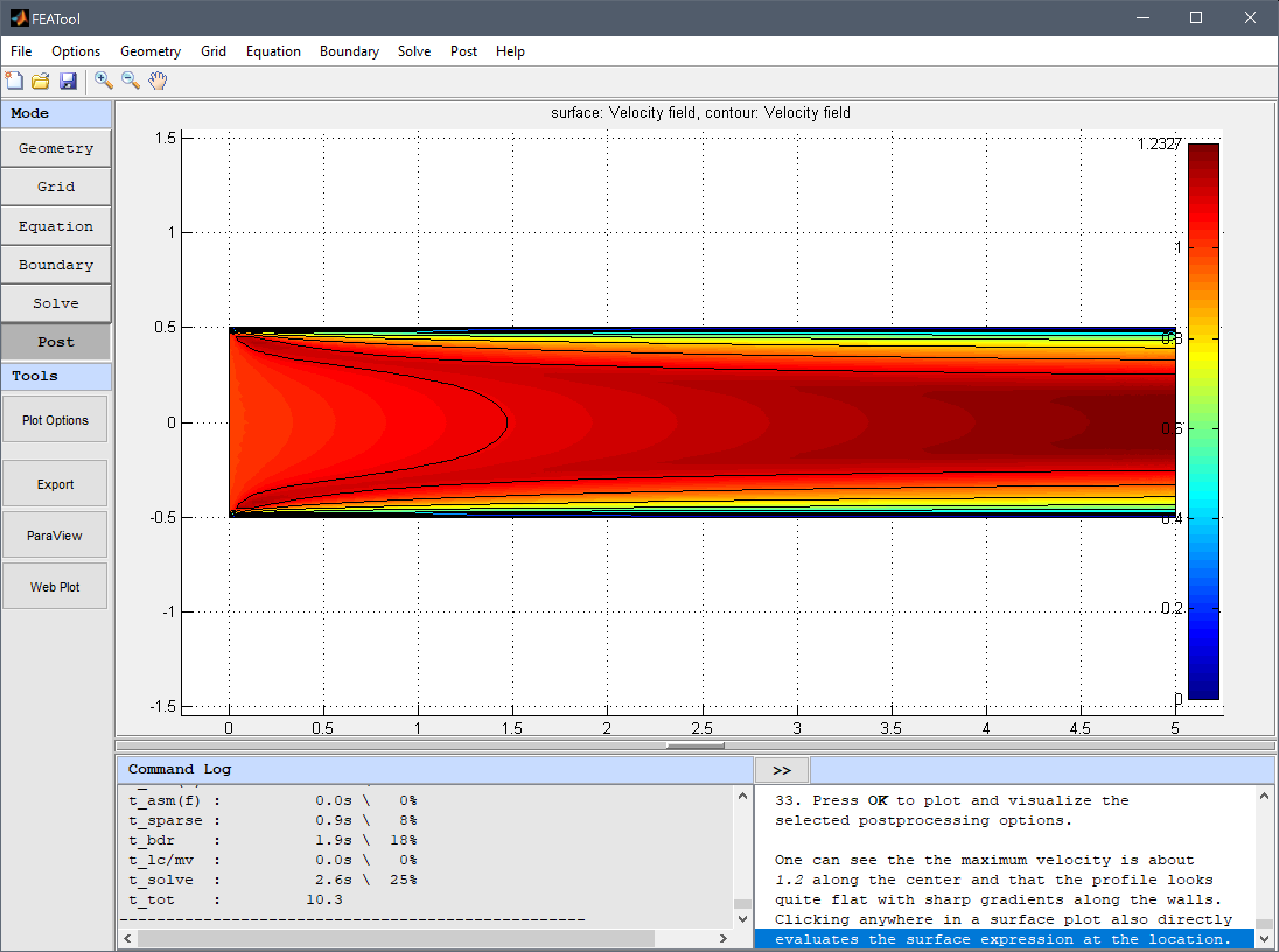
One can see that the maximum velocity is about 1.2 along the center and that the profile looks quite flat with sharp gradients along the walls. Clicking anywhere in a surface plot also directly evaluates the surface expression at the location.
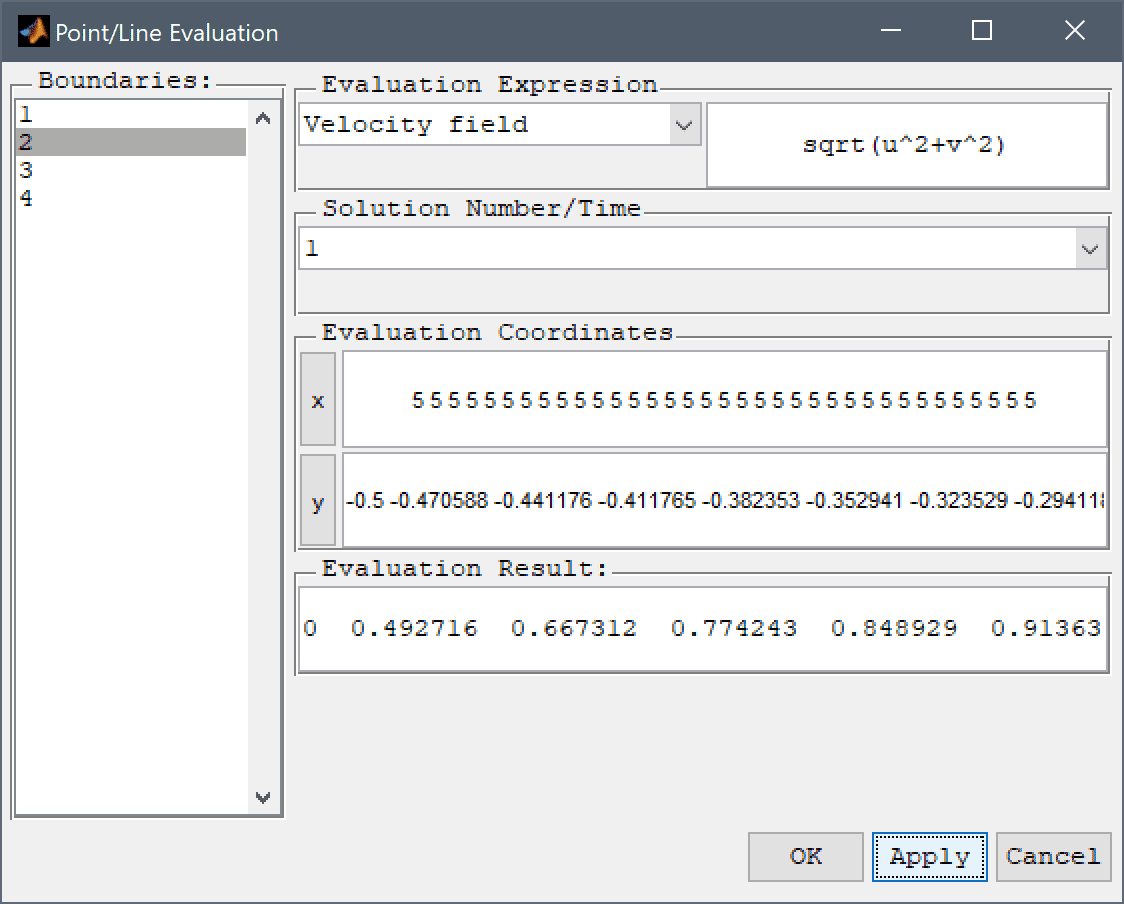
The Point/Line Evaluation menu option can be used to plot a cross section which can show the shape of the turbulent velocity profile more clearly.
Select 2 in the Boundaries list box.
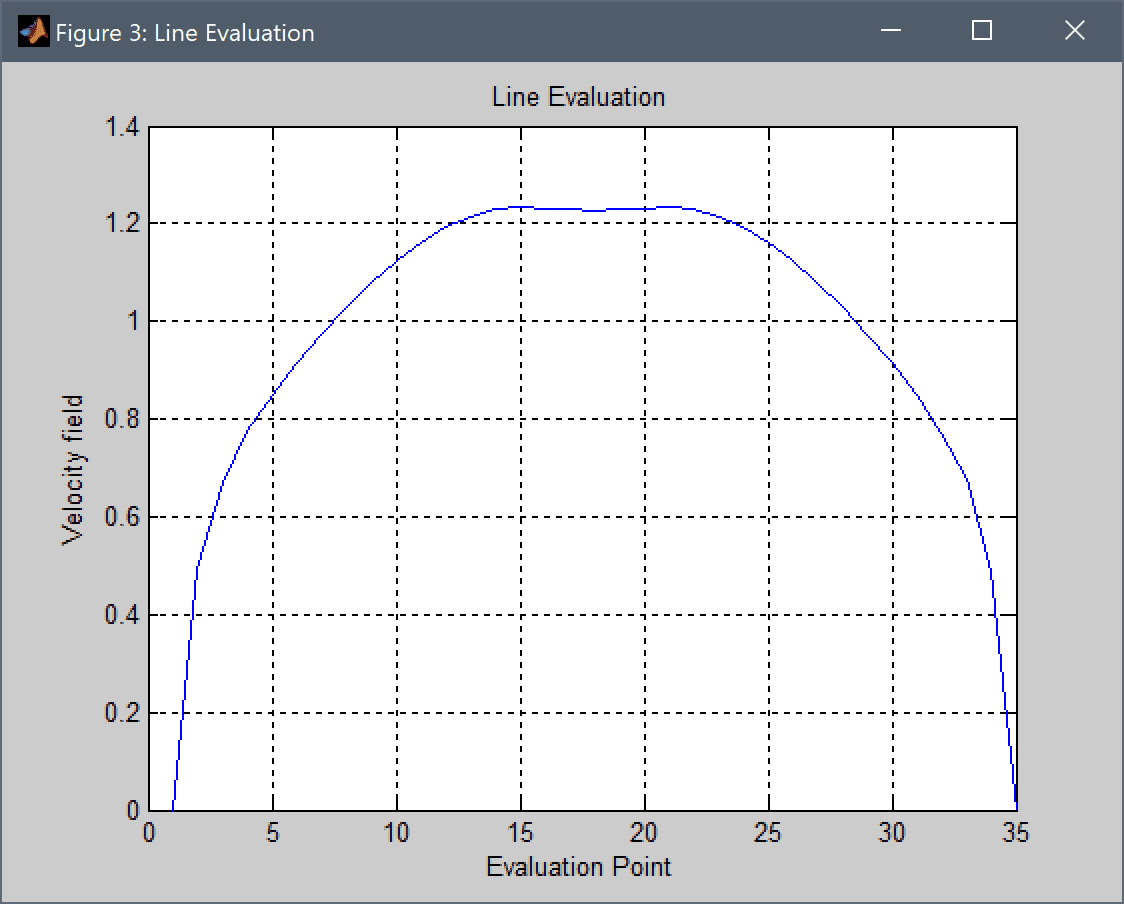
The resulting turbulent velocity profile agrees quite well with the experimental results of Laufer, J. (1950).
A custom expression for the turbulence viscosity will be defined and incorporated so that the total viscosity equals the molecular plus the turbulent viscosity.
Enter 1/Re + miu_t into the Viscosity edit field.
The expression for the custom mixing length model is here defined as rho*l_mix^2*sqrt(uy^2+vx^2) where the mixing length l_mix is defined as min(kappa*l_wall,0.09*l_char). The von Karman constant kappa is 0.41, l_wall is the minimum distance from the walls, and l_char the characteristic length is taken as the maximum of l_wall.
| Name | Expression |
|---|---|
| kappa | 0.41 |
| l_char | 0.5 |
| l_wall | 0.5-abs(y) |
| l_mix | min(kappa*l_wall,0.09*l_char) |
| miu_t | rho_ns*l_mix^2*sqrt(uy^2+vx^2) |
The new solution with a custom expression for the turbulence model is very similar to both the built-in model and reference.
The turbulent channel flow fluid dynamics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file (available as the example ex_navierstokes17 script file), or GUI script (.fes) file.