
|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|
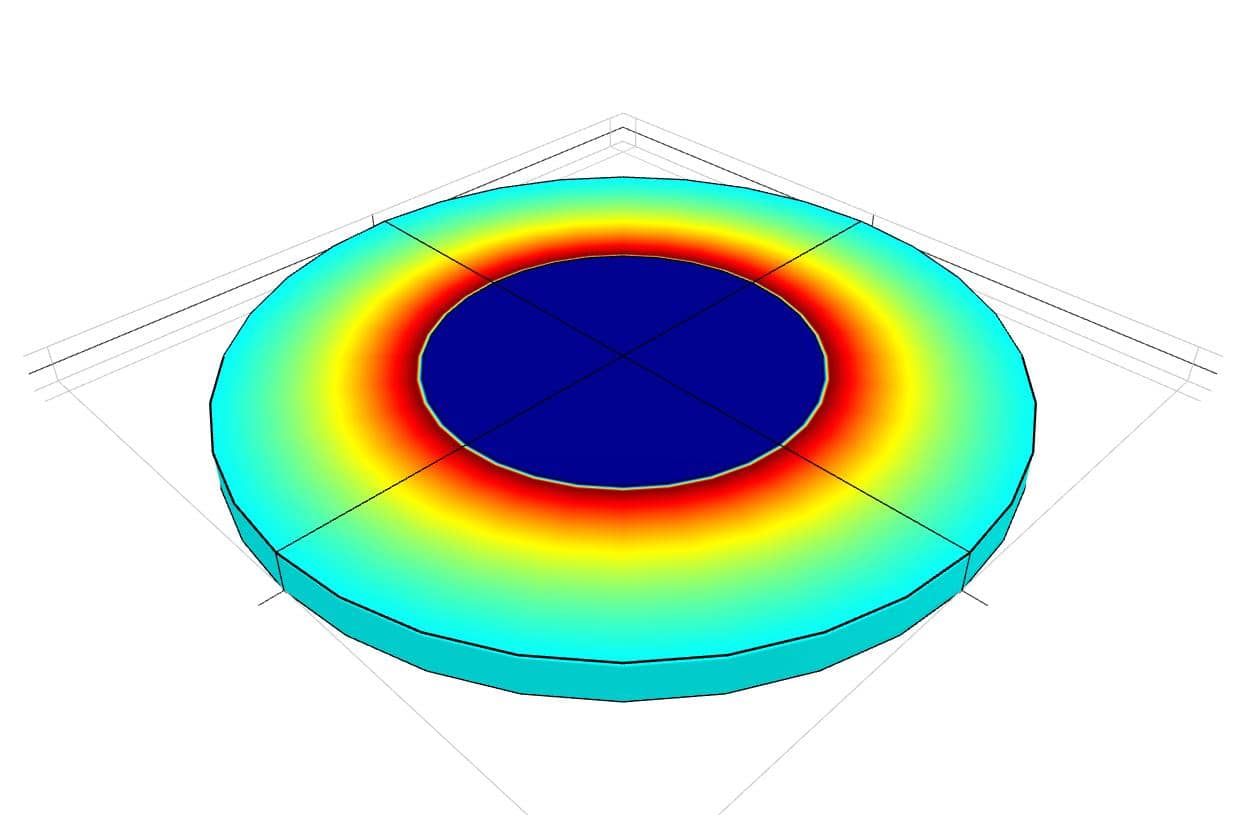
This multiphysics model examines how magnetic forces give rise to stresses in a long thick cylindrical solenoid. A current density of 106 A/m2 is running through a wound coil with 1 cm inner to 2 cm outer radii. The material of the coil is assumed to have a modulus of elasticity of 1.075⋅1011 N/m2 and Poisson's ratio of 0.33, and air occupies the inner hollow core.
As this is a one-way coupled problem, the magnetostatic effects will be solved for first, after which the calculated magnetic forces will be used as input to the stress-strain problem. Due to symmetry it is also sufficient to model a 2D axisymmetric cross-section. The resulting magnetic flux density and circumferential stress at r = 1.3 cm will be compared to the theoretical values of 8.798⋅10-3 T and 96.71 N/m, respectively [1].
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Multiphysics > Stress Distribution in a Solenoid from the File menu. Or alternatively, follow the step-by-step instructions below.
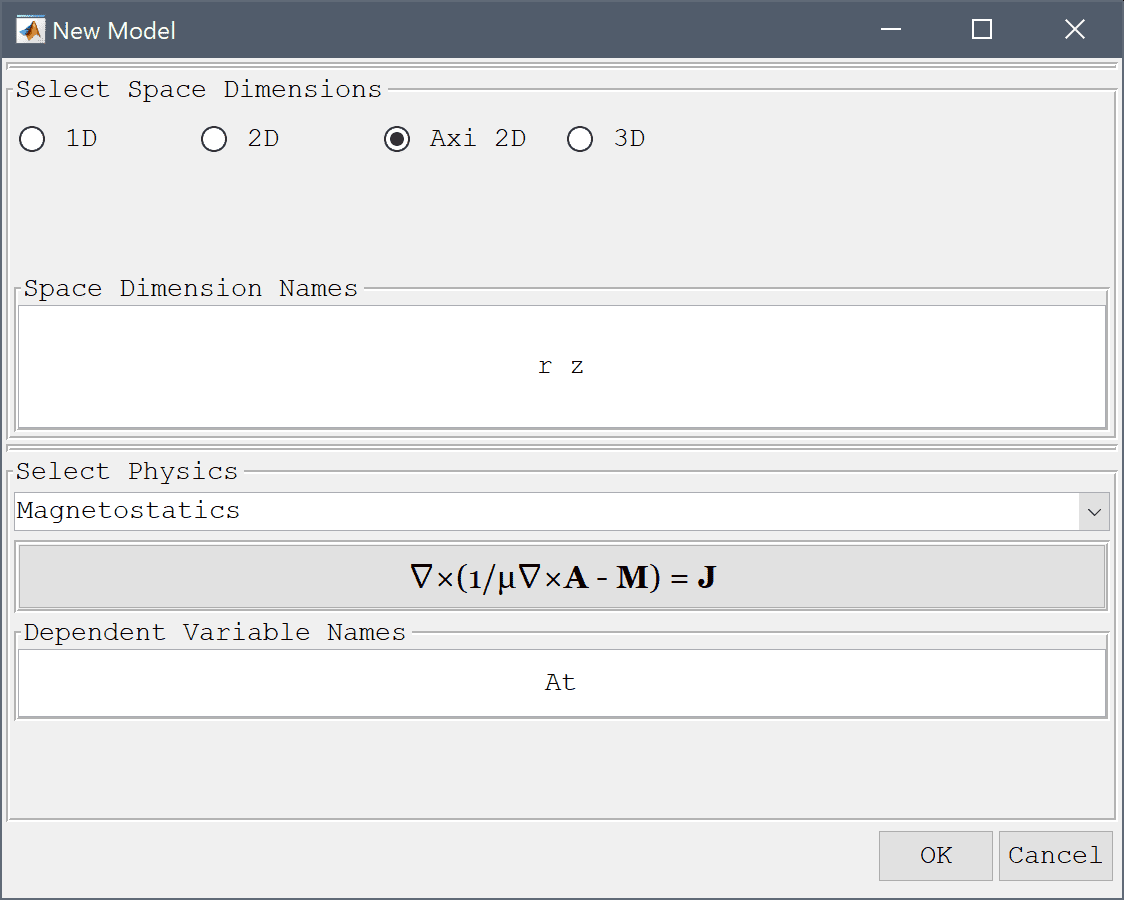
Select the Magnetostatics physics mode from the Select Physics drop-down menu.
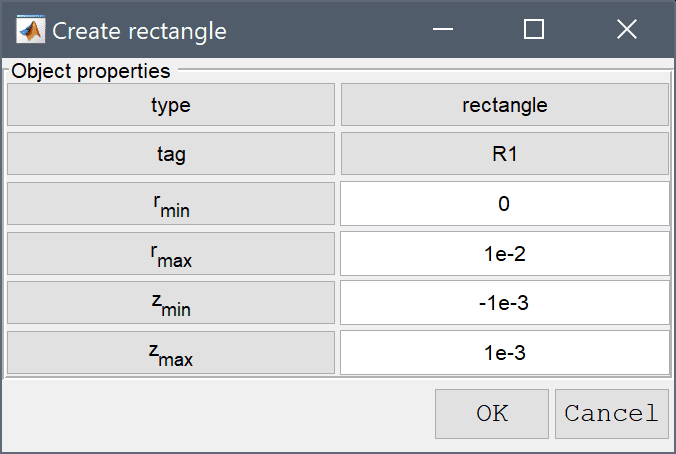
The geometry here consists of two rectangular subdomains the inner air r = 0-1 cm and the solenoid r = 1-2 cm, as the solution is expected to be symmetric in the axial direction the height does not influence the solution.
0 into the xmin edit field.1e-2 into the xmax edit field.-1e-3 into the ymin edit field.Enter 1e-3 into the ymax edit field.
1e-2 into the xmin edit field.2e-2 into the xmax edit field.-1e-3 into the ymin edit field.1e-3 into the ymax edit field.Press OK to finish and close the dialog box.
Equation and material coefficients can be specified in Equation/Subdomain mode. In the Equation Settings dialog box that automatically opens, enter a current density of 106 A/m2 for the second subdomain. The other coefficients can be left to their default values.
Note that FEATool works with any unit system, and it is up to the user to use consistent units for geometry dimensions, material, equation, and boundary coefficients.
0 into the Current density, θ edit field.Enter 1e6 into the Current density, θ edit field.
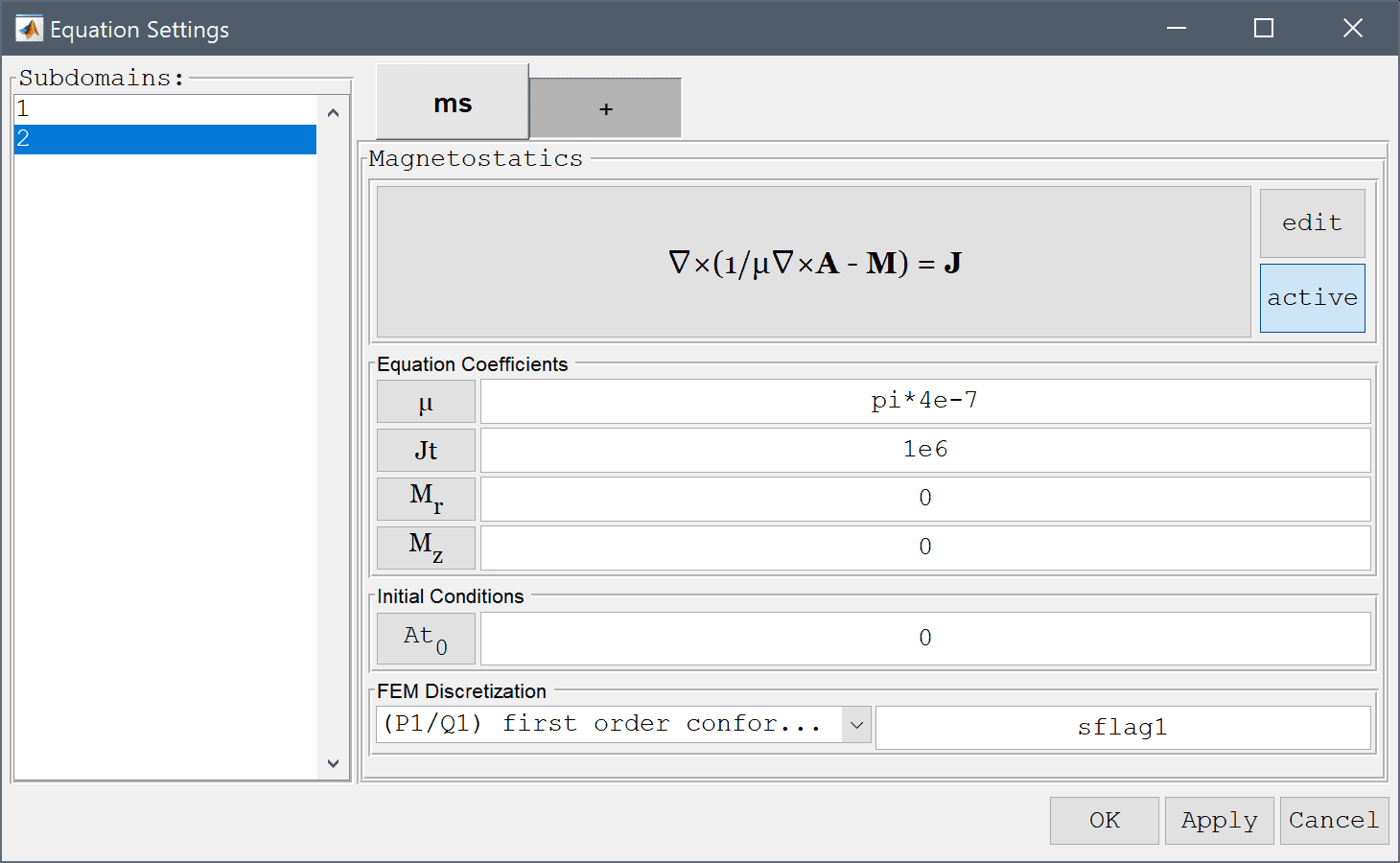
We will add a axisymmetric stress-strain inactive physics mode, to be used in the second solution step.
Press the active toggle button.
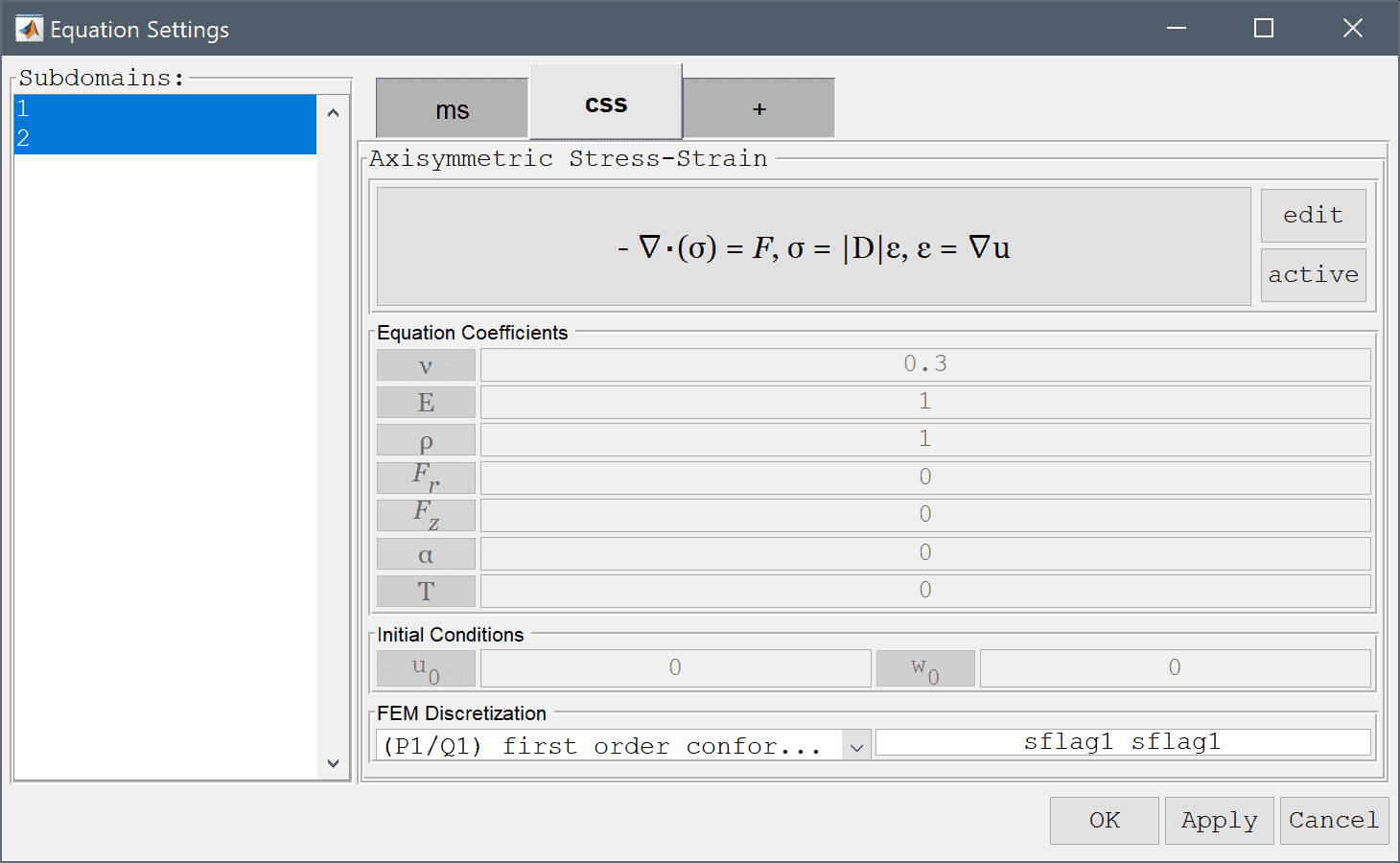
Select Electric insulation/symmetry from the Magnetostatics drop-down menu.
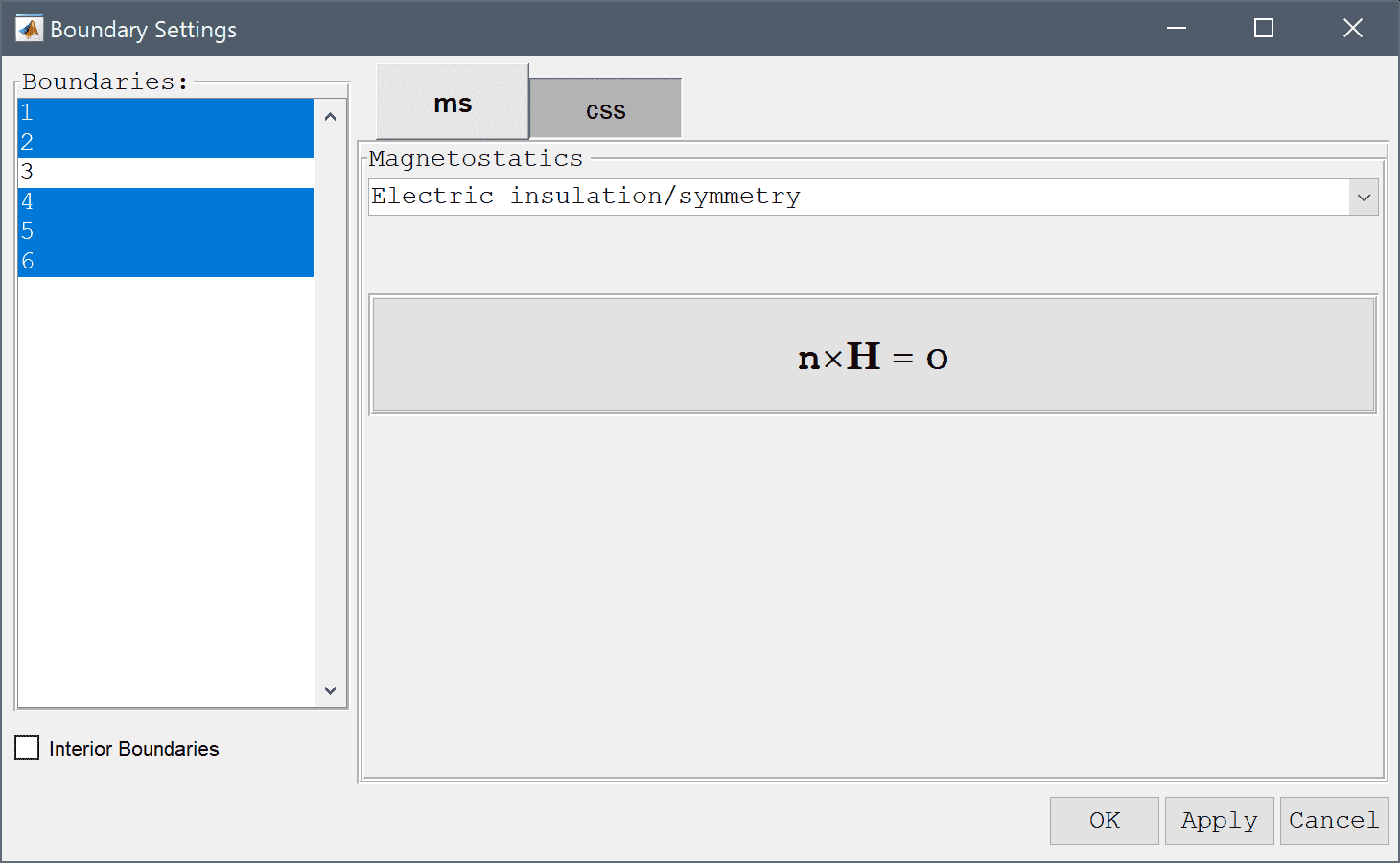
Select the inner boundary and modify the surface current/Neumann boundary coefficient to -2/mu_ms*At in order to manually prescribe a neutral axis Robin boundary condition.
Enter -2/mu_ms*At into the Surface current edit field.
After the problem has been solved FEATool will automatically switch to postprocessing mode and here display the computed magnetic potential. To change the plot, open the postprocessing settings dialog box by clicking on the Plot Options Toolbar button.
25 into the Number or specified vector of contour levels to plot edit field.Press OK to plot and visualize the selected postprocessing options.
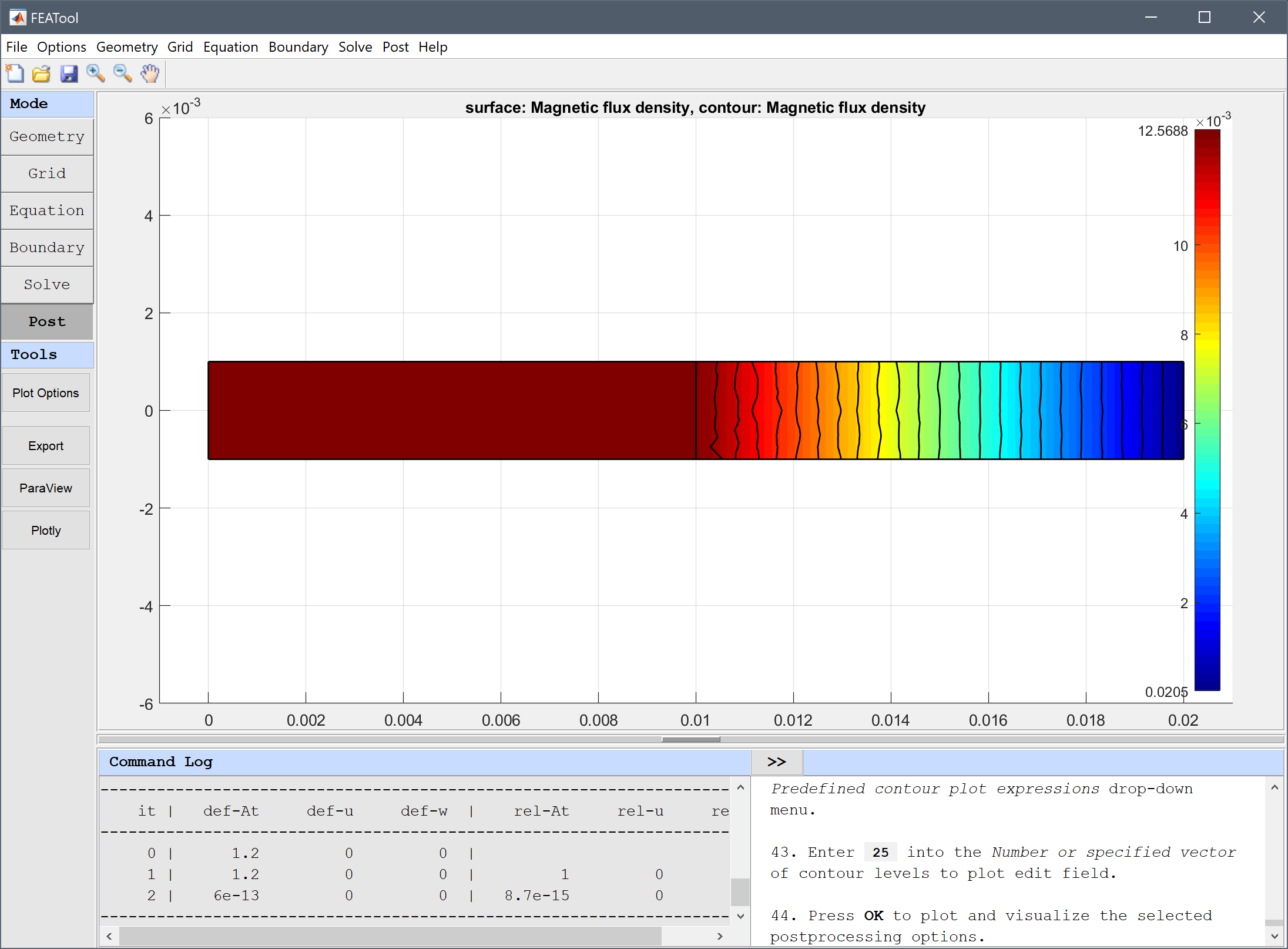
Using the point evaluation tool we can evaluate the flux density to compare with the expected value.
0.013 into the Evaluation coordinates in r-direction edit field.0 into the Evaluation coordinates in z-direction edit field.Press the Apply button.
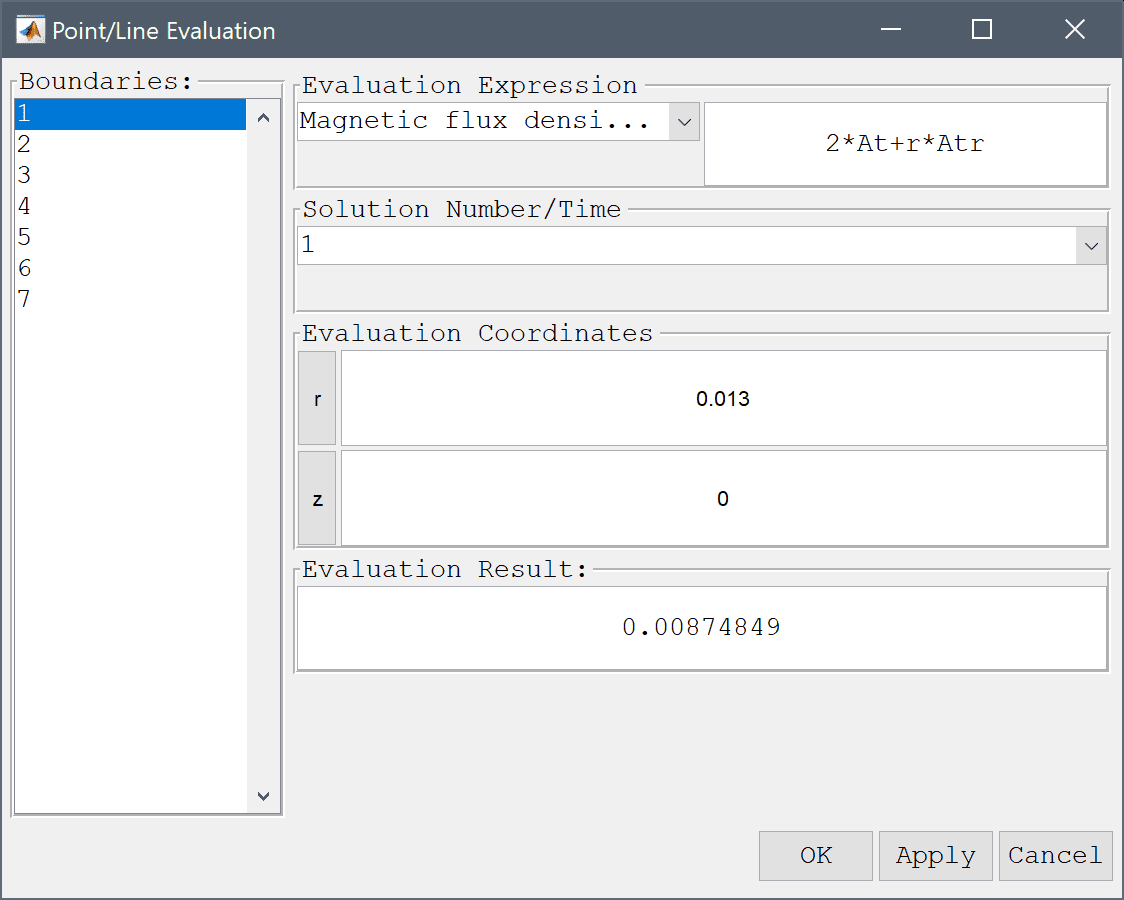
A computed flux density of 8.749e-3 T compares well with the expected value of 8.798e-3 T.
Now in the second step we go back and deactivate the magnetostatics physics mode and activate and solve for the stress-stain. Although we could solve both physics simultaneously, since the model only features a one way coupling, magnetic forces to stress-strain, we can save computational time and cost by solving in two steps.
0.33 into the Poisson's ratio edit field.1.075e11 into the Modulus of elasticity edit field.The resulting magnetic body forces are here due to the product of the current density and B field.
-1e6*(2*At+r*Atr) into the Body load in r-direction edit field.Enter 1e6*(Atz*r) into the Body load in z-direction edit field.
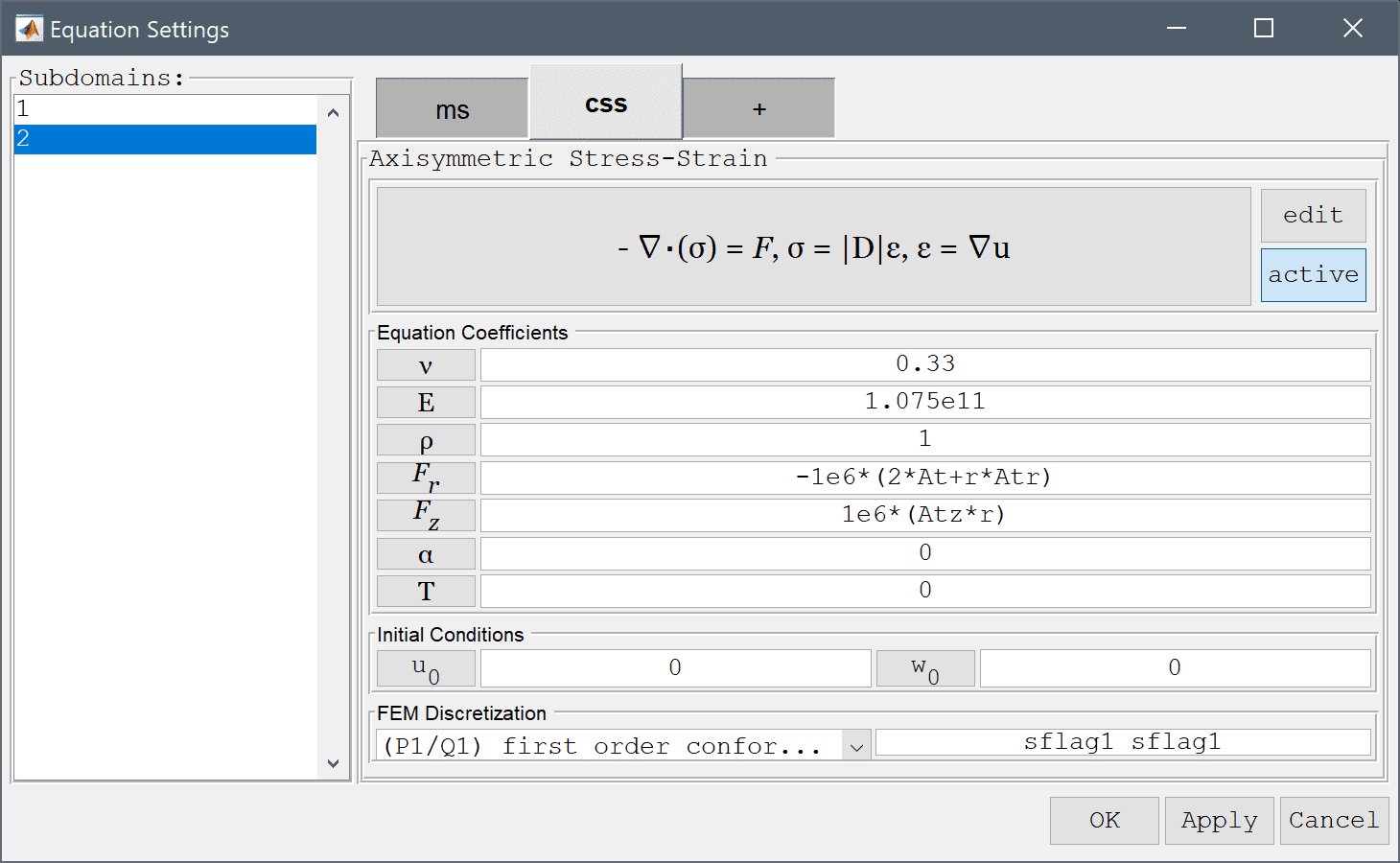
Due to symmetry the z-displacement is fixed at the top and bottom boundaries.
Note that the restart button is used here instead of the solve button = in order to use the existing already computed solution for the magnetic field.
Press OK to plot and visualize the selected postprocessing options.
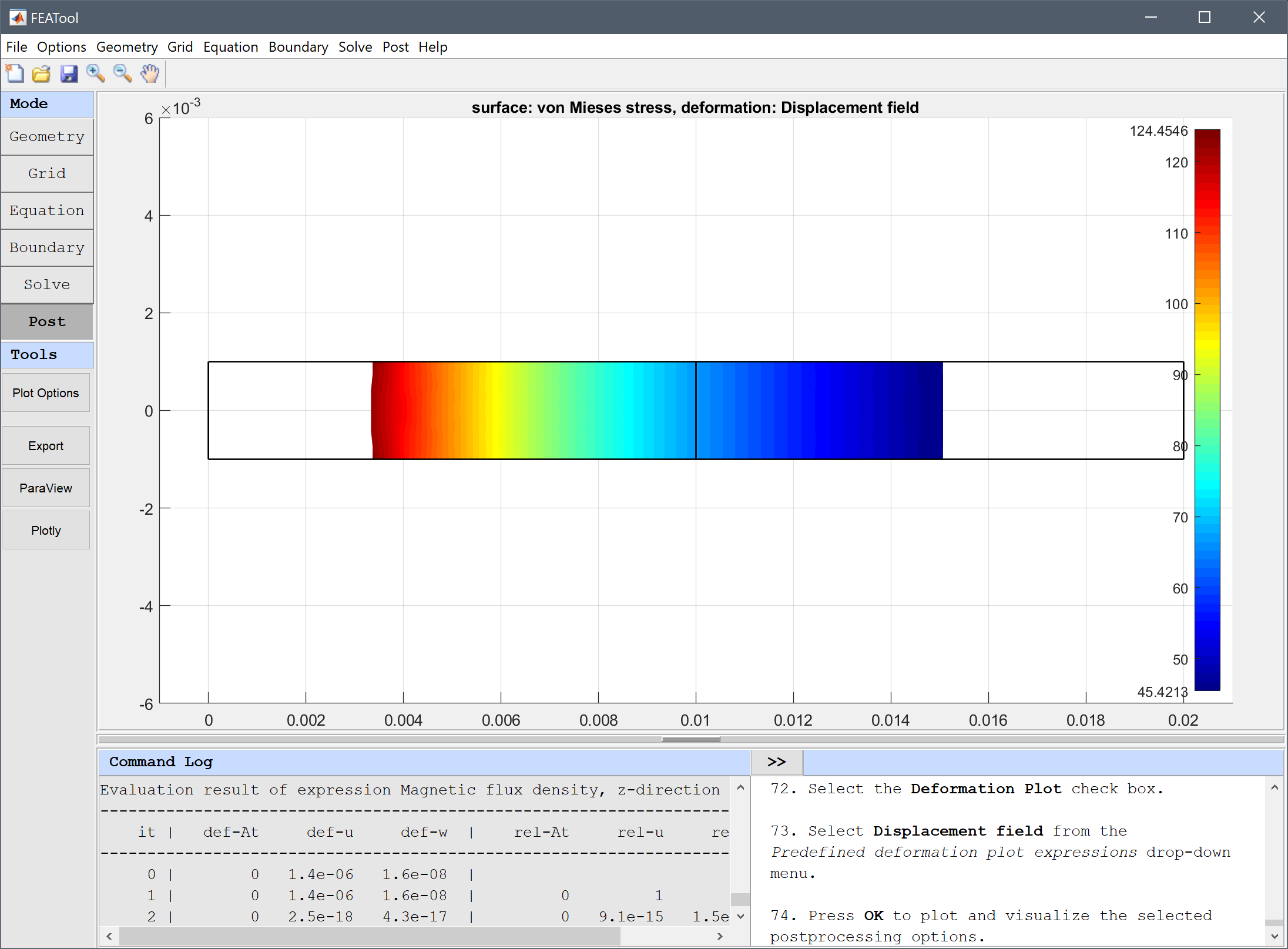
0.013 into the Evaluation coordinates in r-direction edit field.0 into the Evaluation coordinates in z-direction edit field.Press the Apply button.
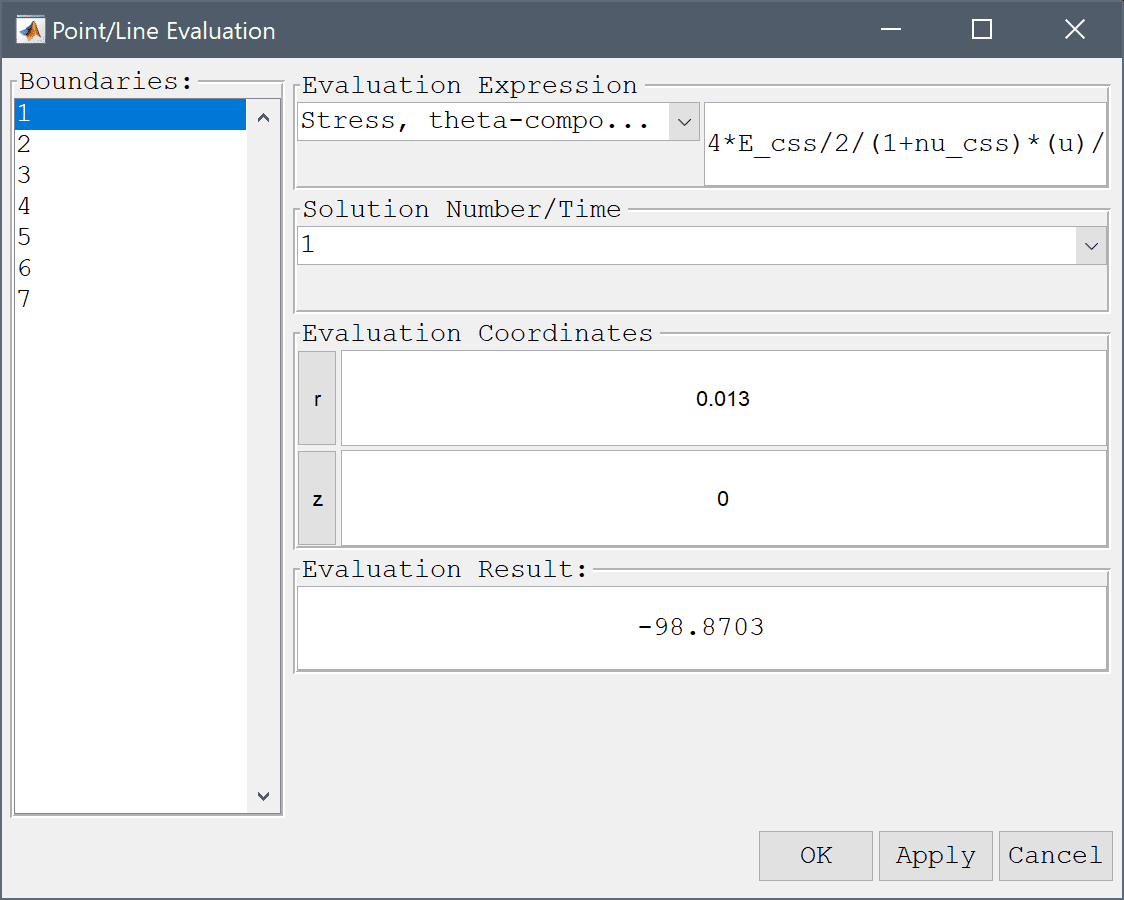
The computed angular stress of 98.87 N/m also compares well with the expected value of 96.71 N/m.
The stress distribution in a solenoid multiphysics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file, or GUI script (.fes) file.
[1] Moon FA. Magneto-Solid Mechanics, Chapter 4, John Wiley & Sons, NY, 1984.