
|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.17.5
Finite Element Analysis Toolbox
|
Saint-Venant shallow water equations is a simplified model of fluid flow with a free surface. The non-conservative form of the equations read
\[ \left\{\begin{array}{l} \frac{\partial h}{\partial t} + (u\frac{\partial h}{\partial x} + v\frac{\partial h}{\partial y} ) + (h+H)(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}) = 0 \\ \frac{\partial u}{\partial t} + (u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} ) = -g\frac{\partial h}{\partial x} \\ \frac{\partial v}{\partial t} + (u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} ) = -g\frac{\partial h}{\partial y} \end{array}\right. \]
where h is the unknown free surface height relative to the mean level H.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Classic PDE > Shallow Water Equations from the File menu, viewed as a videotutorial", or alternatively, follow the step-by-step instructions below.
Both the Custom Equation and Convection and Diffusion physics modes are used in this example.
h into the Dependent Variable Names edit field.0 into the xmin edit field.5 into the xmax edit field.0 into the ymin edit field.1 into the ymax edit field.0.2 into the Grid Size edit field.h' + (u*hx_t + v*hy_t) + (h+H)*(ux_t+vy_t) = 0, into the edit field for the h equation.0.2*exp(-((x-4)^2)) into the edit field for the Initial condition for h.Now add two Convection and Diffusion physics modes for the horizontal velocity components u and v. Although the Custom Equation physics mode could also be used here, the Convection and Diffusion physics modes feature pre-defined equations, and convective stabilization which is necessary here.
u into the Dependent Variable Names edit field.0 into the Diffusion coefficient edit field.u into the Convection velocity in x-direction edit field.v into the Convection velocity in y-direction edit field.-g*hx into the Reaction rate edit field.v into the Dependent Variable Names edit field.0 into the Diffusion coefficient edit field.u into the Convection velocity in x-direction edit field.v into the Convection velocity in y-direction edit field.-g*hy into the Reaction rate edit field.Two constants also have to be defined, one for the mean fluid level H = 1, and one for the gravitational constant g = 9.8.
The height h should not be constrained, and should therefore be prescribed with homogeneous Neumann conditions everywhere.
The right boundary is assumed to be a wall, and zero velocities are therefore prescribed there. The top and bottom boundaries are assumed to be symmetric, and feature zero flow in the normal direction.
Select the Time-Dependent solver with the following parameters.
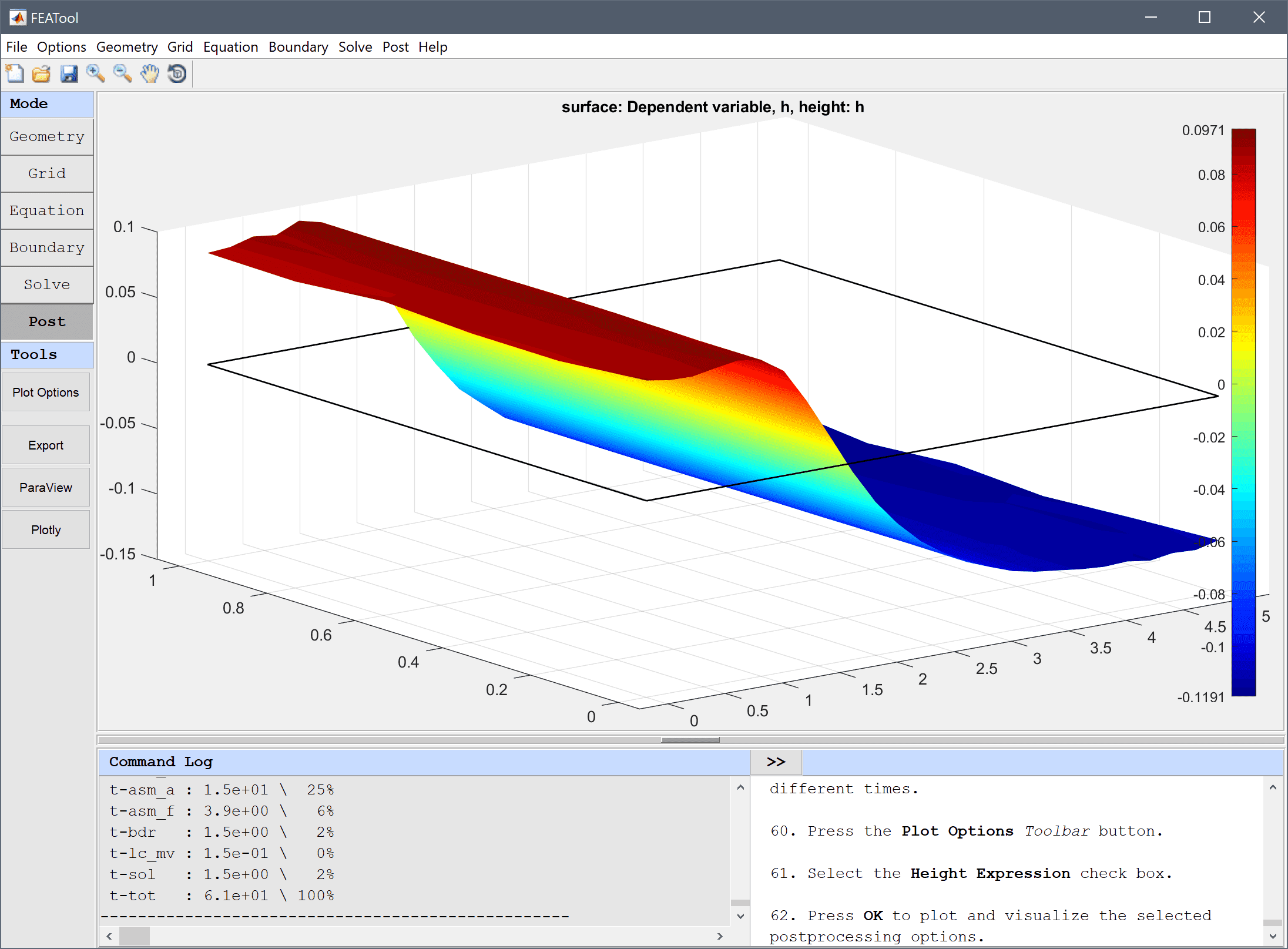
0.001 into the Non-linear stopping criteria for solution differences (changes) between iterations edit field.0.01 into the Time step size edit field.1.5 into the Duration of time-dependent simulation (maximum time) edit field.Once the solver has finished, turn on the height plot for h and visualize the free surface for different times.
One can also use the Animate/Playback Solution... option in the Post menu, to create an animation or video of the solution.
The shallow water equations fluid dynamics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file, or GUI script (.fes) file.