
|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|
Calculation of the inviscid flow field around a NACA airfoil using the potential equation. The potential or Laplace equation is equivalent to Poisson equation with a zero source term. Boundary conditions are set as zero normal flow on the airfoil body, and unit velocity magnitude at the external boundaries of the domain.
This model is available as an automated tutorial by selecting Model Examples and Tutorials... > Fluid Dynamics > Potential Flow Over an Airfoil from the File menu, viewed as a video tutorial, or alternatively, follow the step-by-step instructions below.
phi into the Dependent Variable Names edit field.0012 into the series edit field.0 into the angle edit field.100 into the resolution edit field.0.5 0 into the center edit field.1.5 into the xradius edit field.1.5 into the yradius edit field.0.3 in the Subdomain Grid Size edit field and 0.3 0.3 0.3 0.3 0.05 0.05 for the Boundary Grid Size. This will ensure that the airfoil boundaries are resolved with fine grid cells, while the rest of the domain uses a coarse grid.0, and also select (P2/Q2) second order conforming for the FEM Discretization order to ensure that the velocities (which are derivatives of the potential) are represented with high accuracy.A convenient way to define and store coefficients, variables, and expressions is using the Model Constants and Expressions functionality. The defined expressions can then be used in point, equation, boundary coefficients, as well as postprocessing expressions, and can easily be changed and updated in a single place.
| Name | Expression |
|---|---|
| u | phix |
| v | phiy |
| U | sqrt(u^2+v^2) |
| alfa | 0 |
| uinf | cos(alfa*pi/180) |
| vinf | sin(alfa*pi/180) |
| cp | 1-U^2/(uinf^2+vinf^2) |
For potential flow normal velocities can naturally be prescribed as Neumann boundary conditions. Set the flow at the exterior boundaries to nx*uinf+ny*uinf, and airfoil boundaries to zero (where nx and ny will be evaluated as the unit normal vectors of the boundaries).
nx*uinf+ny*vinf into the Neumann coefficient edit field.0 into the Neumann coefficient edit field.One also has to set a reference level for the potential phi at one of the points, in order to ensure a unique solution for stationary problems without any Dirichlet/prescribed value boundary conditions.
0 into the corresponding constraint expression edit field for the potential phi. Press OK to finish and close the dialog box.The potential function is displayed by default. Open the Postprocessing settings dialog box and visualize the velocity field U as surface, contour, and arrow plots instead.
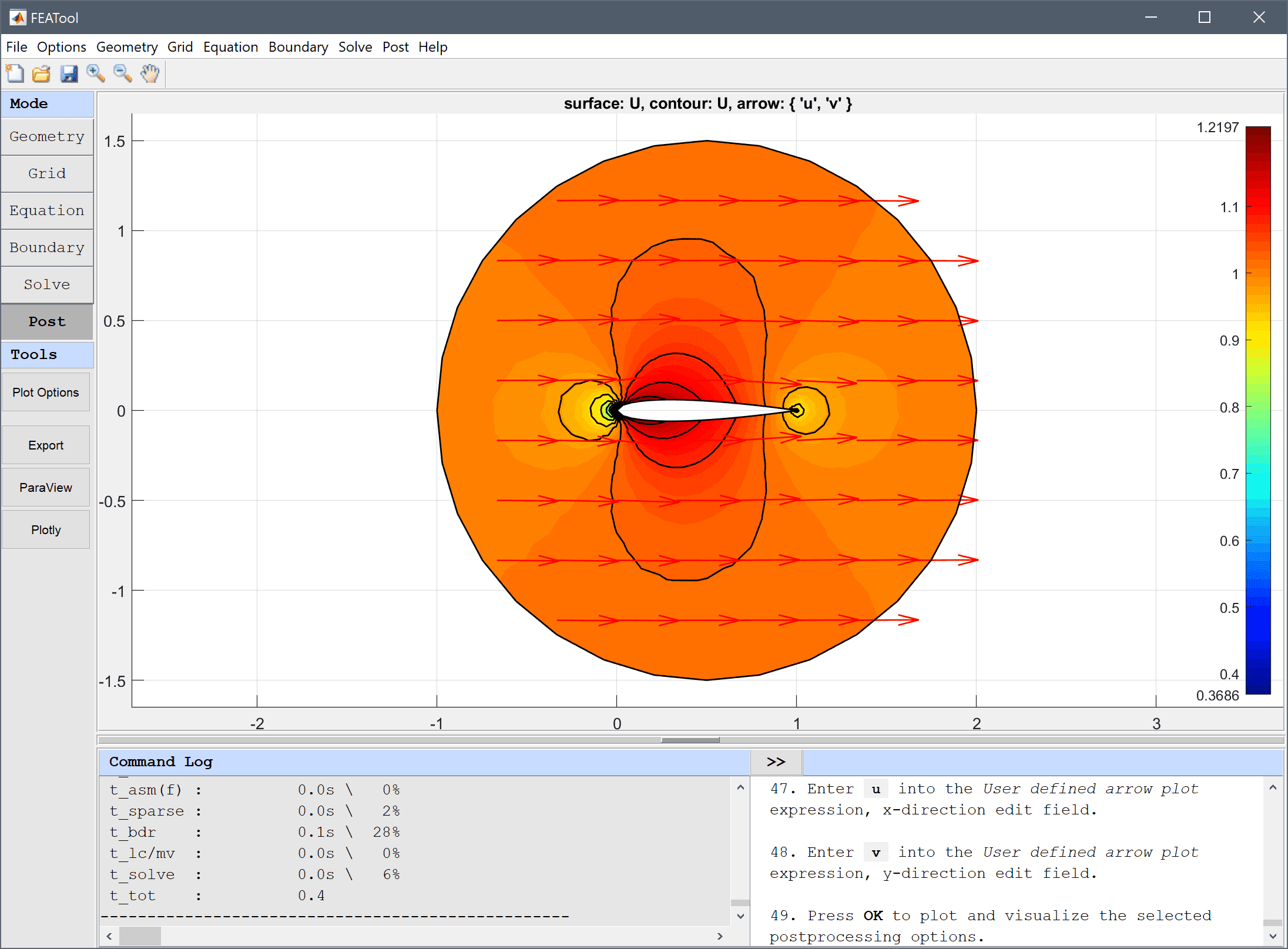
U into the User defined surface plot expression edit field.U into the User defined contour plot expression edit field.20 into the Number or specified vector of contour levels to plot edit field.u into the User defined arrow plot expression, x-direction edit field.v into the User defined arrow plot expression, y-direction edit field.Use the Point/Line Evaluation functionality to plot the pressure coefficient cp along the upper wing boundary. At the stagnation point at the left edge the pressure coefficient should be close to 1, it then rapidly jumps towards -0.5 as the flow quickly accelerates, after which it slowly increases towards the trailing edge.
cp into the edit field.To see how a higher angle of attack effects the flow field, change the previously defined constant alfa and solve the model again.
6 degrees into the expression edit field for the angle of attack, alfa.Note that the flow field now is unsymmetric with two stagnation points. As the viscosity and the Kutta condition at the trailing edge is not accounted for in this model, the second stagnation point is found at the rear top boundary of the airfoil instead of at the trailing edge as would typically be expected.
The potential flow over an airfoil fluid dynamics model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file (available as the example ex_potential_flow1 script file), or GUI script (.fes) file.