
|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|

|
FEATool Multiphysics
v1.18.0
Finite Element Analysis Toolbox
|
The following example models shrink fitting of a two part assembly. A chilled tungsten rod is inserted into a slot in a heated steel frame. The rod can be fitted due to thermal expansion of the frame, and when the assembly reaches equilibrium temperature the two parts will be joined due to the ensuing pressure fit.
This model illustrates how to simulate the transient heat transfer process with two domains of different materials. The assembly is cooled due to convection through a surrounding medium kept at Tinf = 17 °C, and the time when the maximum temperature has reached 70 °C should be determined.
FEATool allows for modeling heat transfer through both conduction, that is heat transported by a diffusion process, and also convection, which is heat transported by a fluid due to a flow field. The heat transfer physics mode supports both these processes, and is defined by the following equation
\[ \rho C_p\frac{\partial T}{\partial t} + \nabla\cdot(-k\nabla c) + \rho C_p\mathbf{u}\cdot\nabla T = Q \]
where \(\rho\) is the density, \(C_p\) the heat capacity, \(k\) is the thermal conductivity, \(Q\) heat source term, and \(\mathbf{u}\) a vector valued convective velocity field.
Here, the surrounding cooling medium is not modeled directly, the convective term in the heat transfer equation can therefore be dropped, and the cooling effects are incorporated into the model by using natural convection boundary conditions instead. By not directly modeling the surrounding medium significant computational savings can be made.
This section describes how to set up and solve the thermal shrink fitting example with the FEATool graphical user interface (GUI). The model is available as an automated tutorial by selecting Model Examples and Tutorials... > Heat Transfer > Shrink Fitting of an Assembly from the File menu, viewed as a videotutorial", or alternatively, follow the step-by-step instructions below.
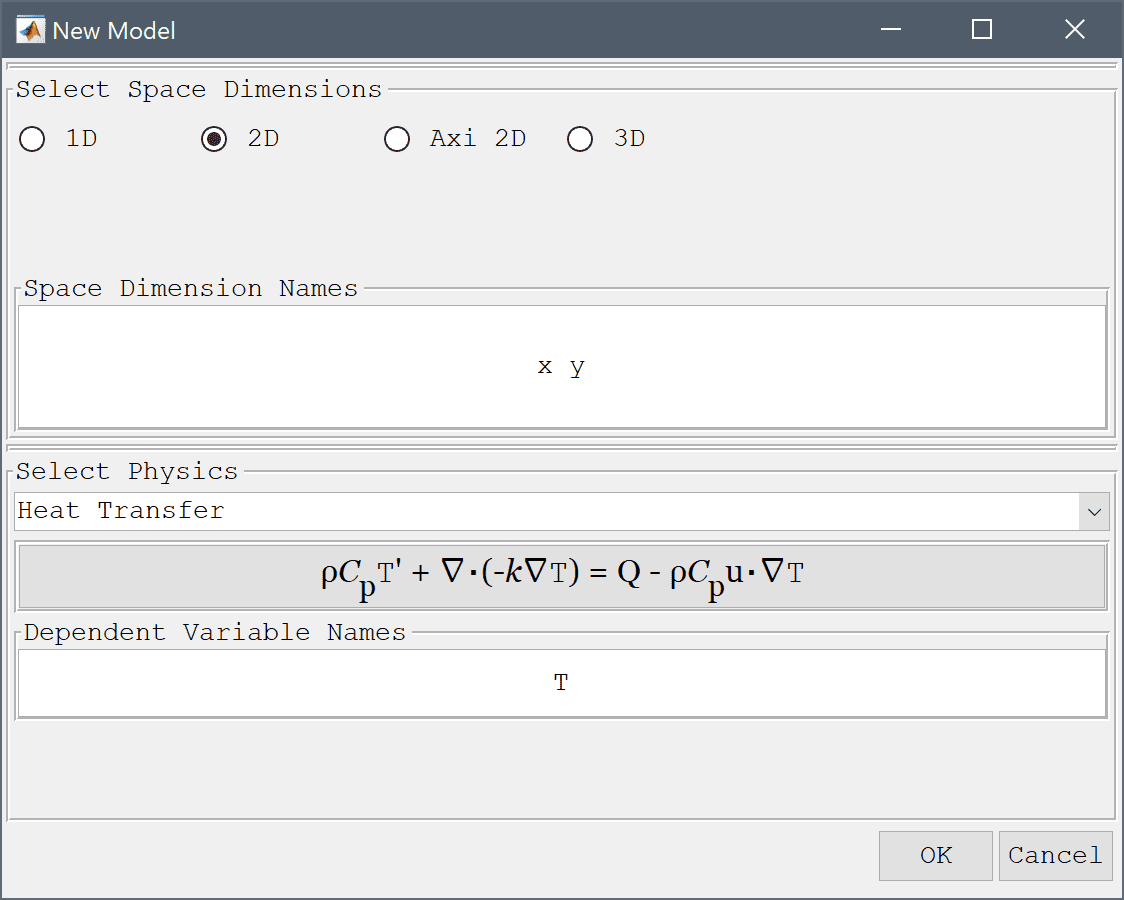
Select the Heat Transfer physics mode from the Select Physics drop-down menu.
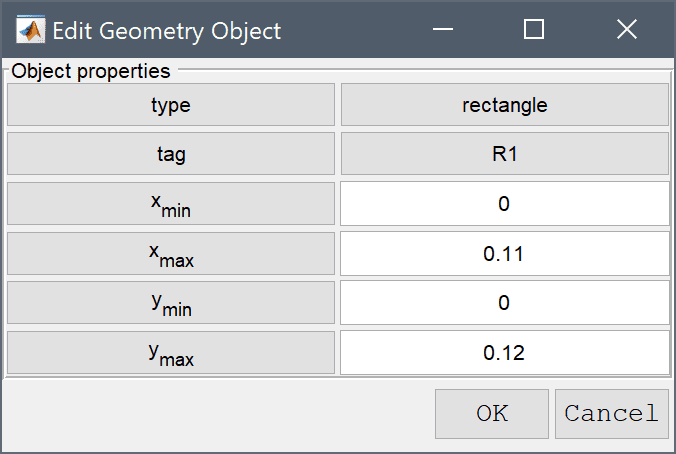
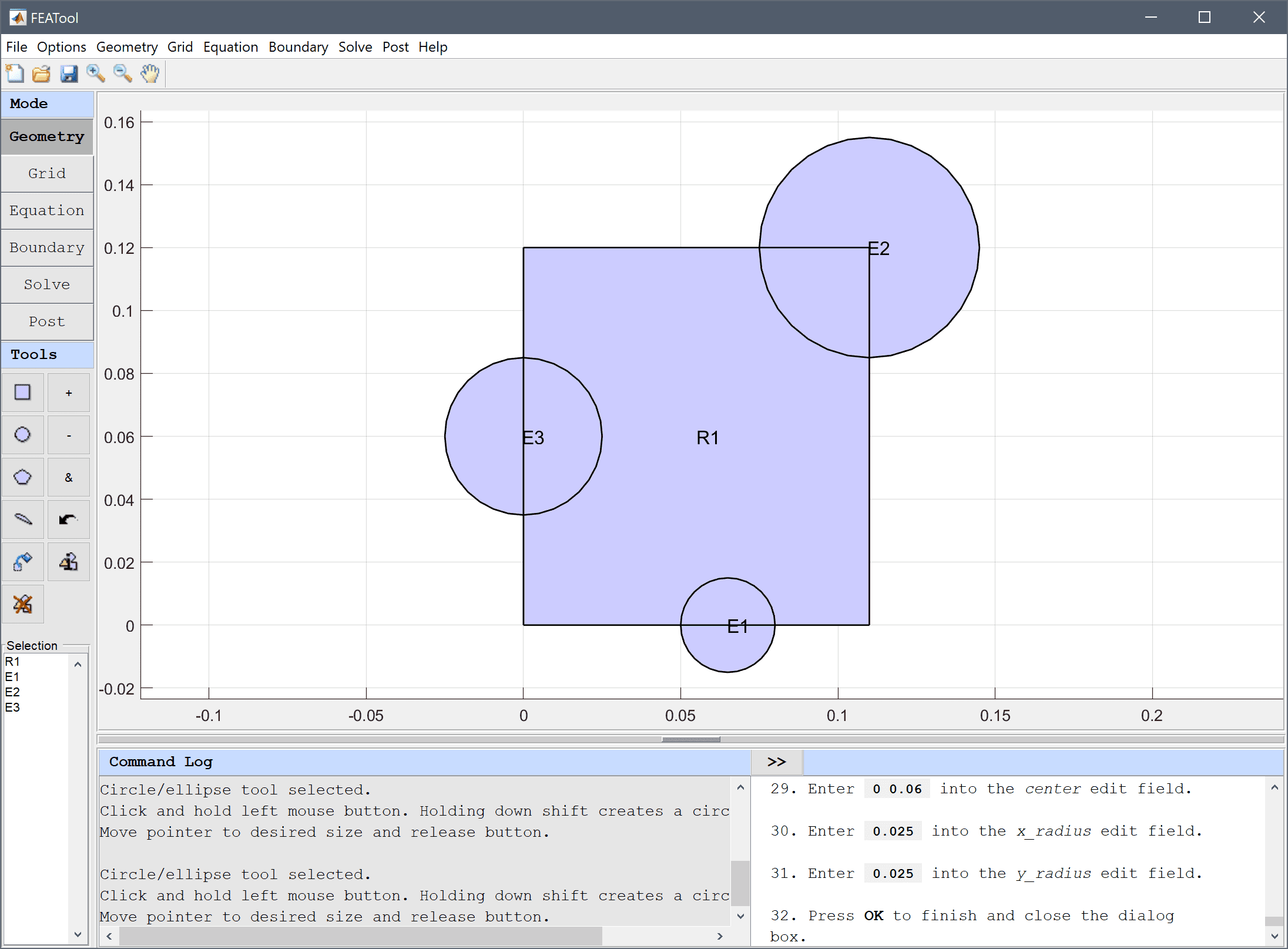
The model geometry consists of a cross section of the frame and rod. The frame can be generated by first creating a rectangle, and then removing three circles and the space for the slot.
0 into the xmin edit field.0.11 into the xmax edit field.0 into the ymin edit field.Enter 0.12 into the ymax edit field.
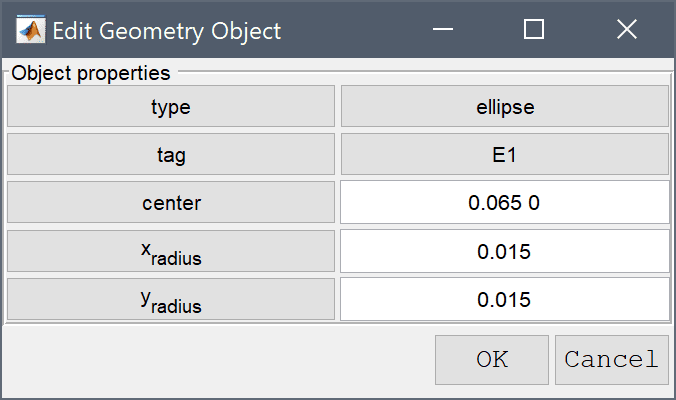
Now create the three circles which are to be removed from R1.
0.065 0 into the center edit field.0.015 into the xradius edit field.Enter 0.015 into the yradius edit field.
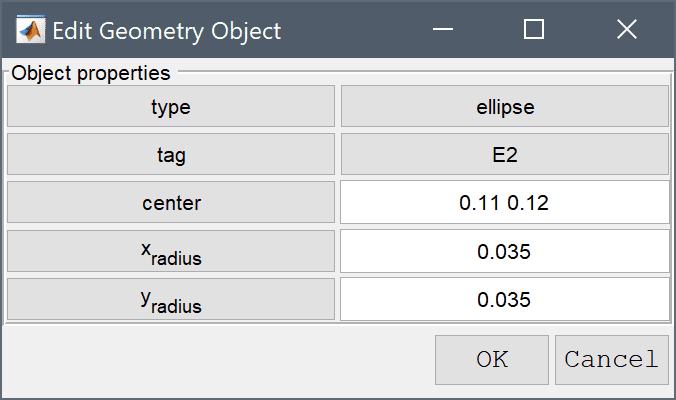
0.11 0.12 into the center edit field.0.035 into the xradius edit field.Enter 0.035 into the yradius edit field.
0 0.06 into the center edit field.0.025 into the xradius edit field.Enter 0.025 into the yradius edit field.
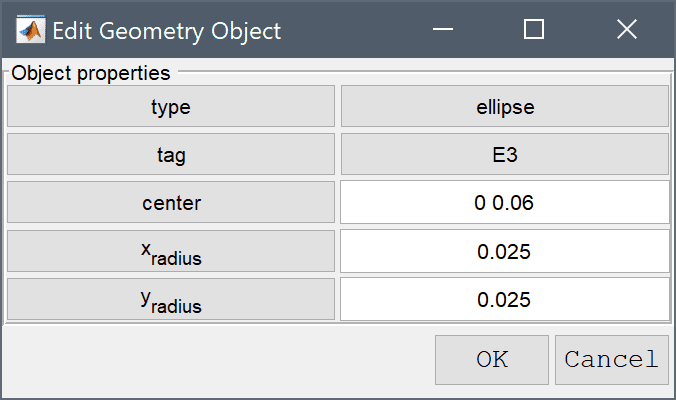
Press OK to finish and close the dialog box.
Enter R1 - E1 - E2 - E3 into the Geometry Formula edit field.
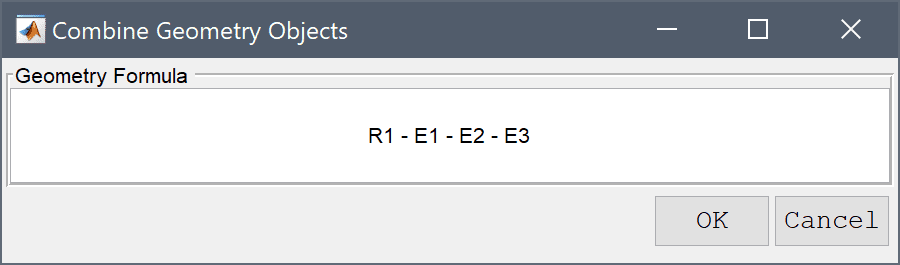
Press OK to finish and close the dialog box.
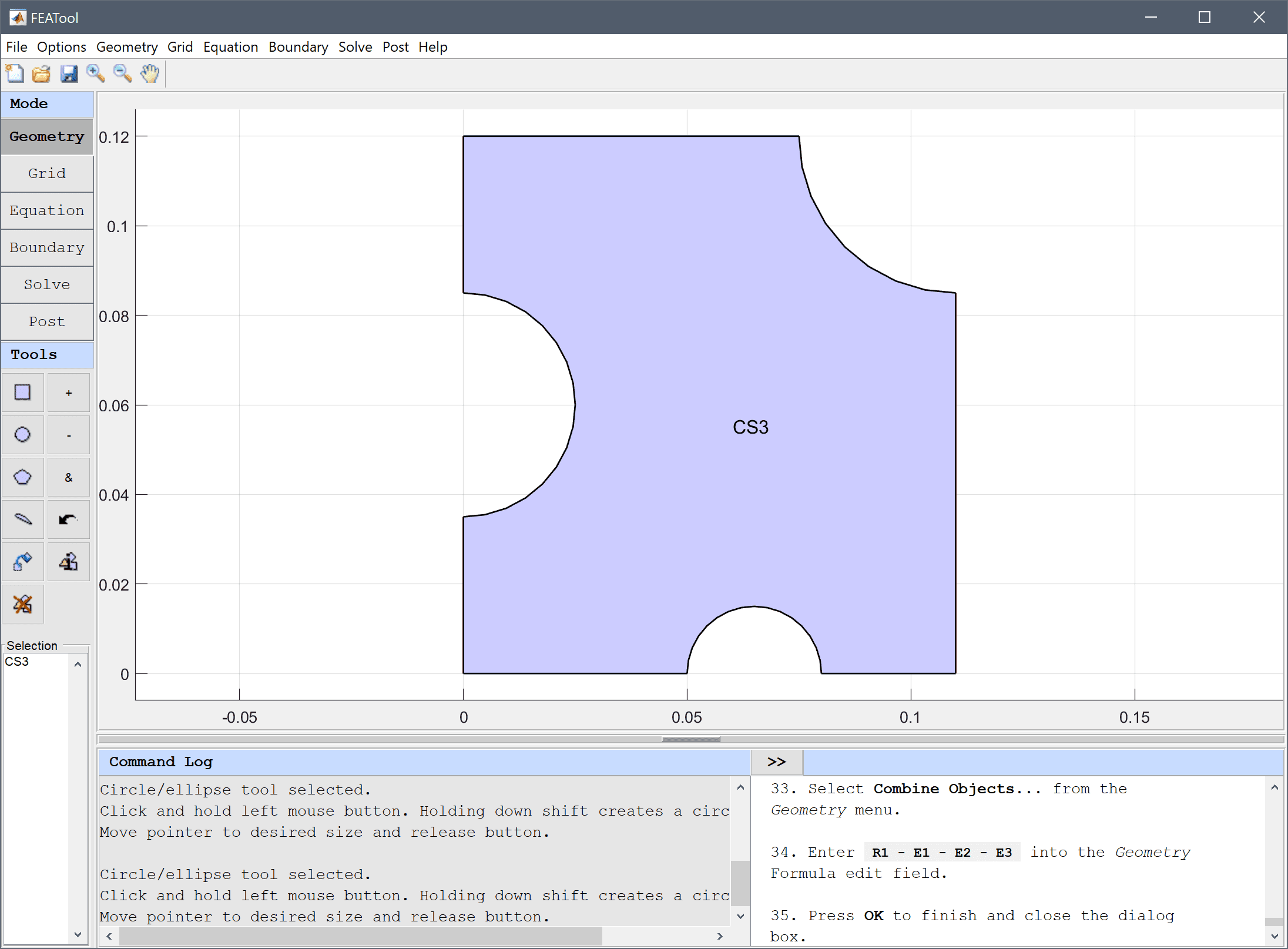
Now we need to create the geometry for the rod by joining a smaller rectangle and a circle.
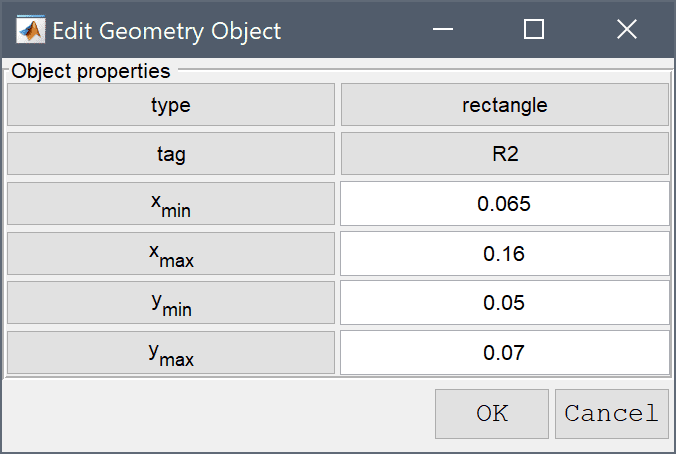
0.065 into the xmin edit field.0.16 into the xmax edit field.0.05 into the ymin edit field.Enter 0.07 into the ymax edit field.
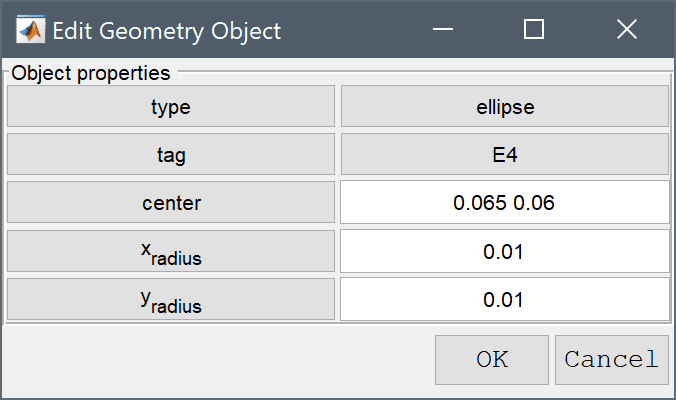
0.065 0.06 into the center edit field.0.01 into the xradius edit field.Enter 0.01 into the yradius edit field.
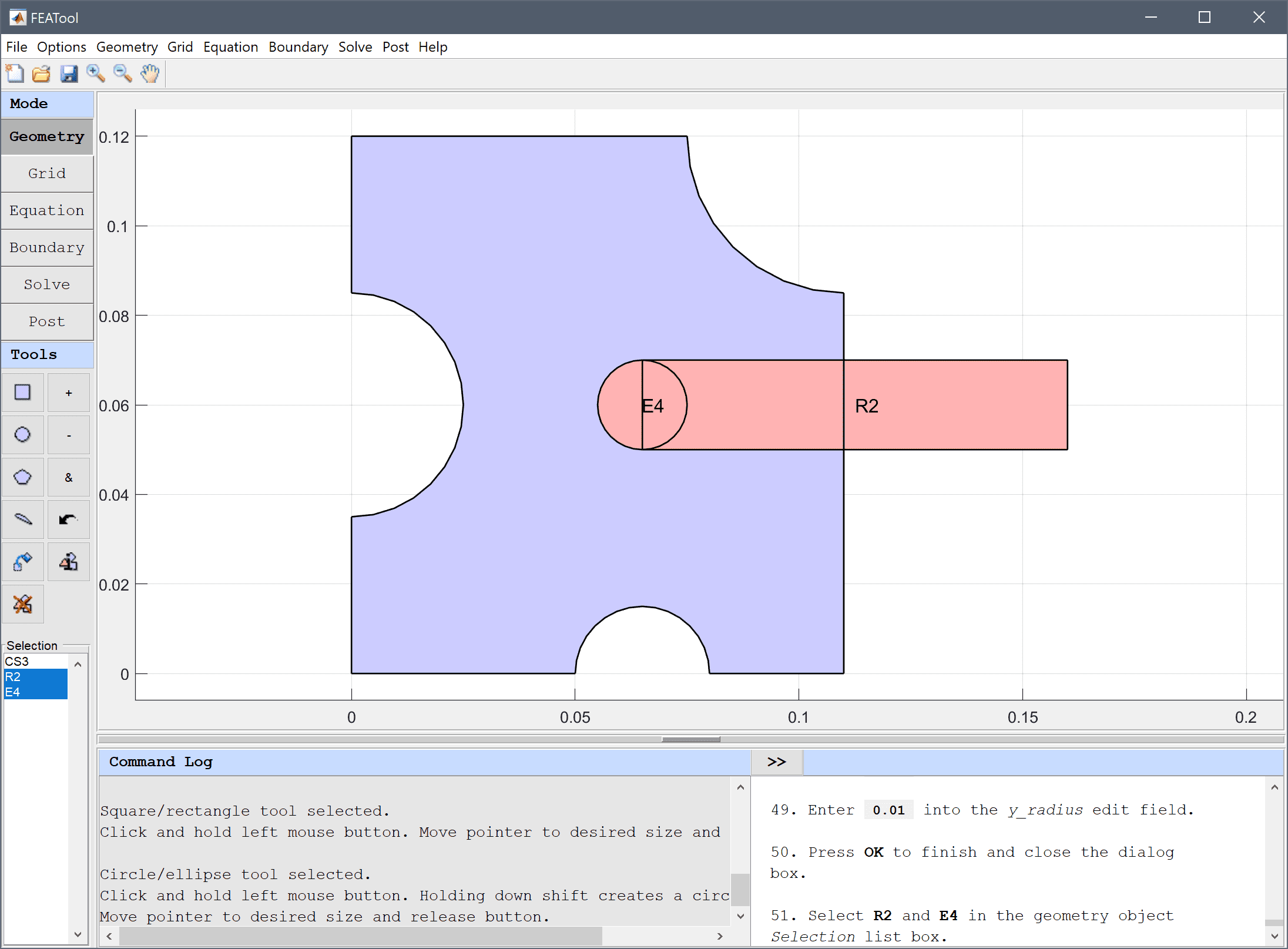
Select R2 and E4 in the geometry object Selection list box.
To make a slot in the frame for the rod, first copy it and subtract the copy from the frame.
Select the Make copy of geometry object check box.
Select CS1 and CJ1 in the geometry object Selection list box.
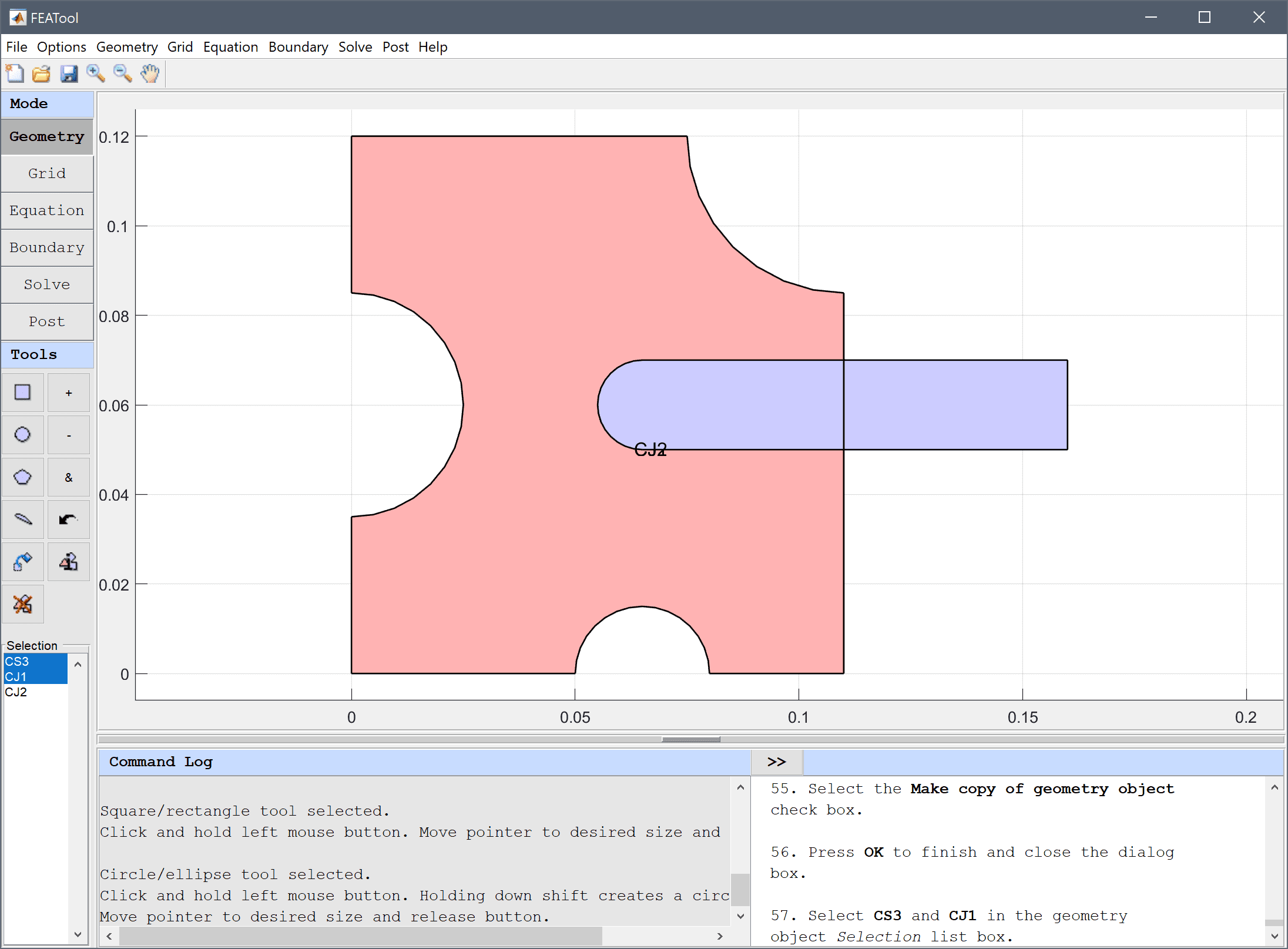
Press the - / Subtract geometry objects Toolbar button.
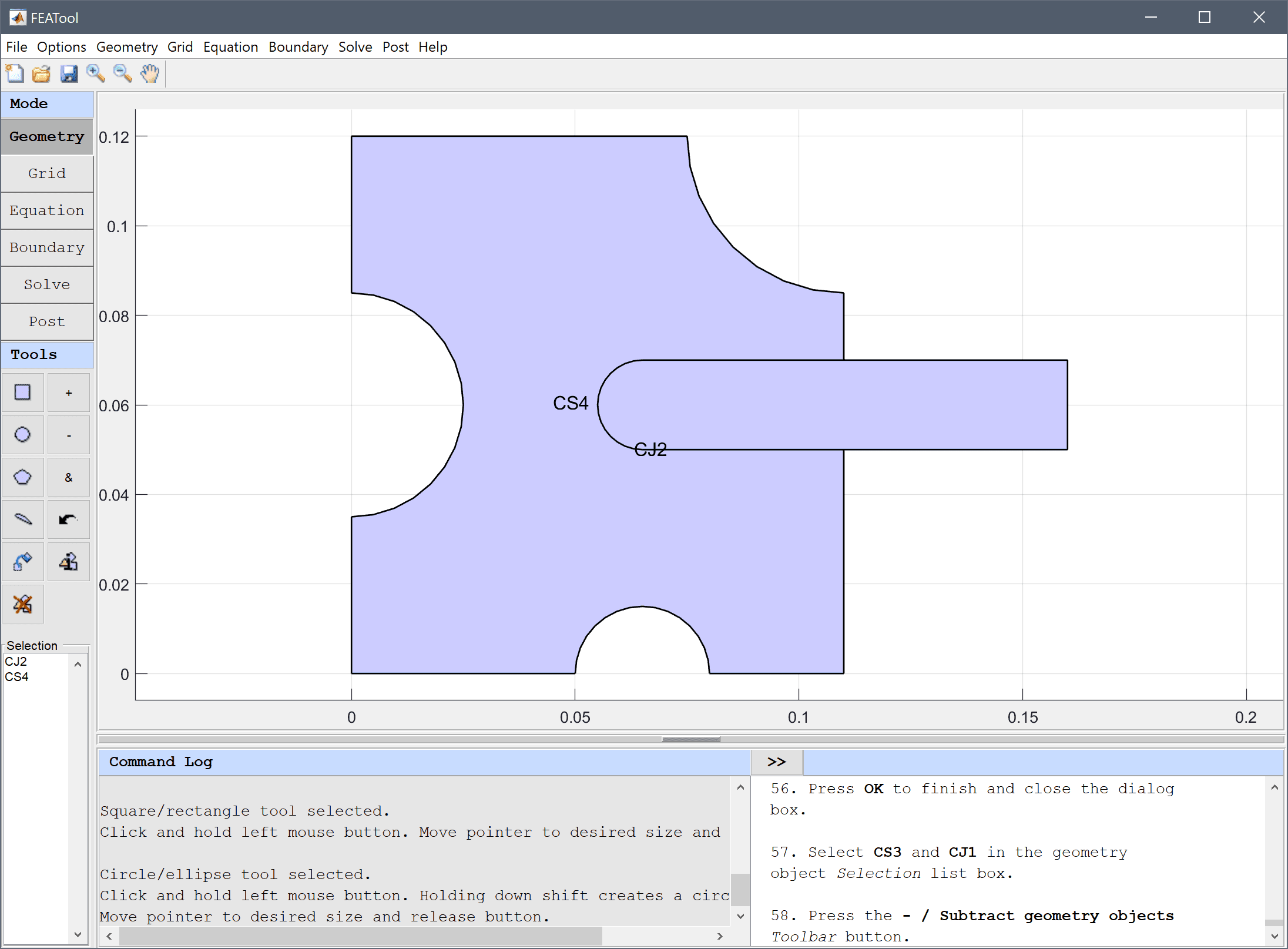
The final geometry consists of two geometry objects, one domain for the frame, and one for the rod.
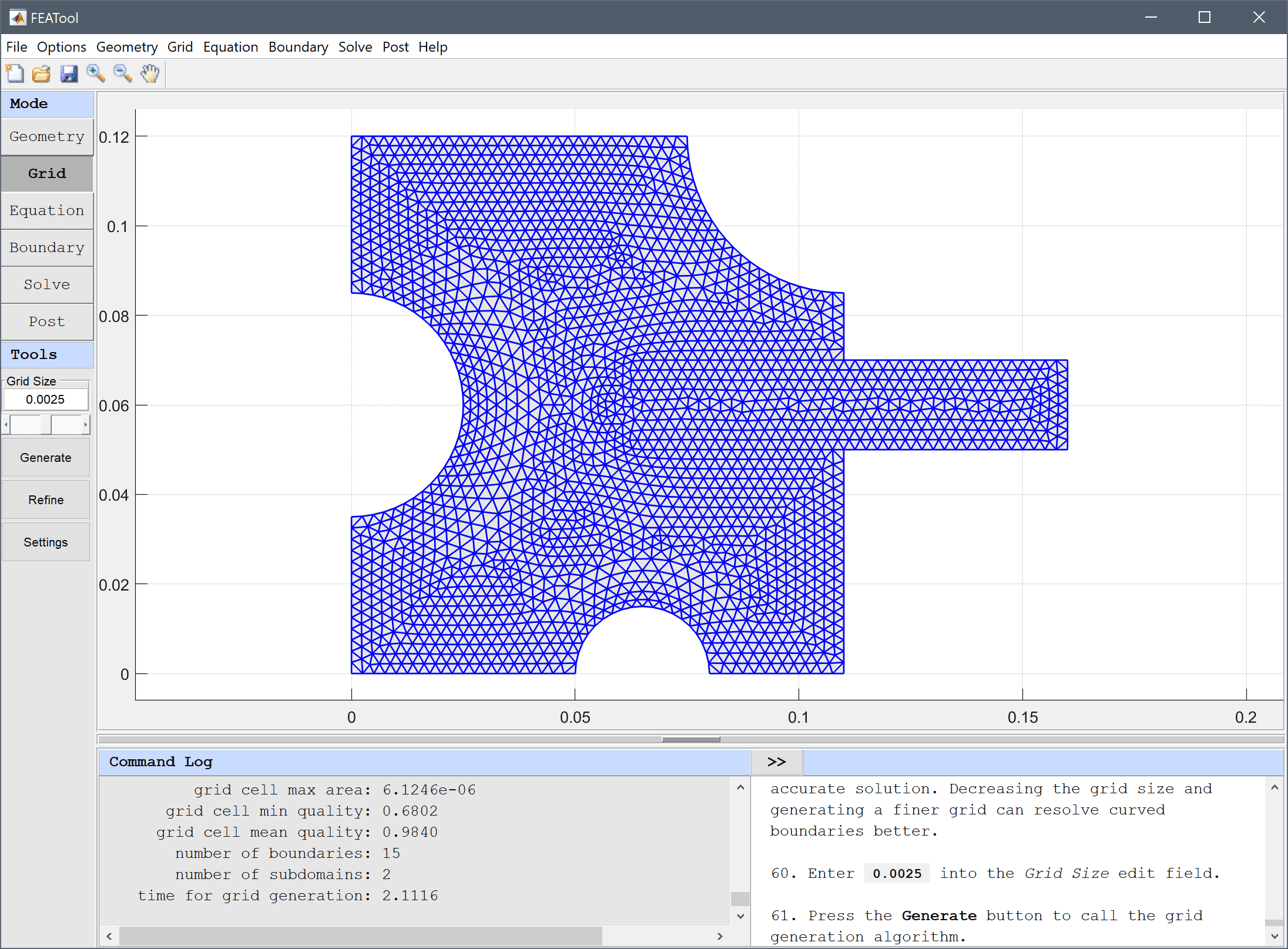
The default grid may be too coarse to ensure an accurate solution. Decreasing the grid size and generating a finer grid can resolve curved boundaries better.
Enter 0.0025 into the Grid Size edit field and press the Generate button to call the grid generation algorithm.
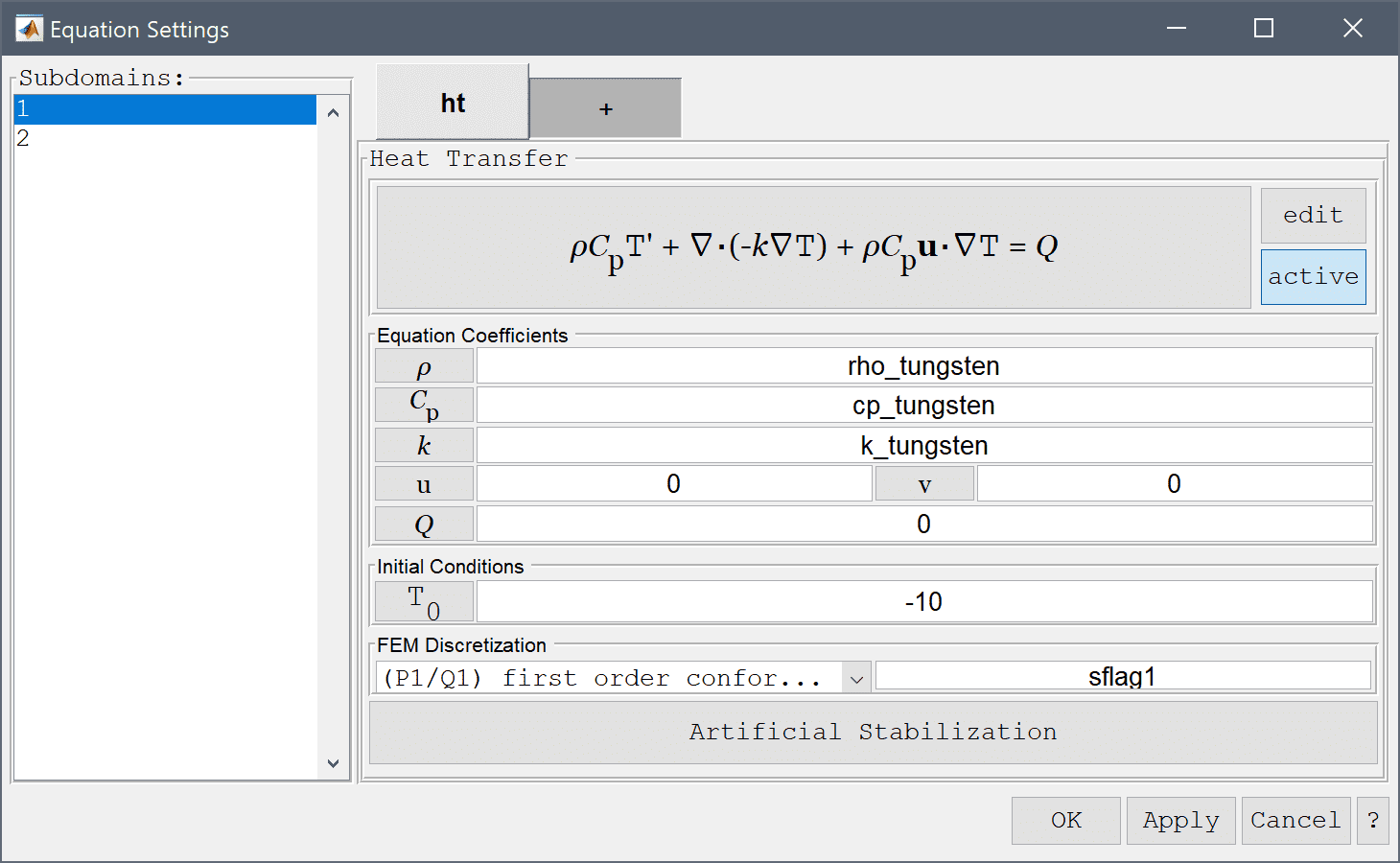
Equation and material coefficients are specified in Equation/Subdomain mode. In the Equation Settings dialog box enter the coefficients for density, heat capacity, thermal conductivity, and initial temperature for each material.
rho_tungsten into the Density edit field.cp_tungsten into the Heat capacity edit field.k_tungsten into the Thermal conductivity edit field.Enter -10 into the Initial condition for T edit field.
rho_steel into the Density edit field.cp_steel into the Heat capacity edit field.k_steel into the Thermal conductivity edit field.Enter 84 into the Initial condition for T edit field.
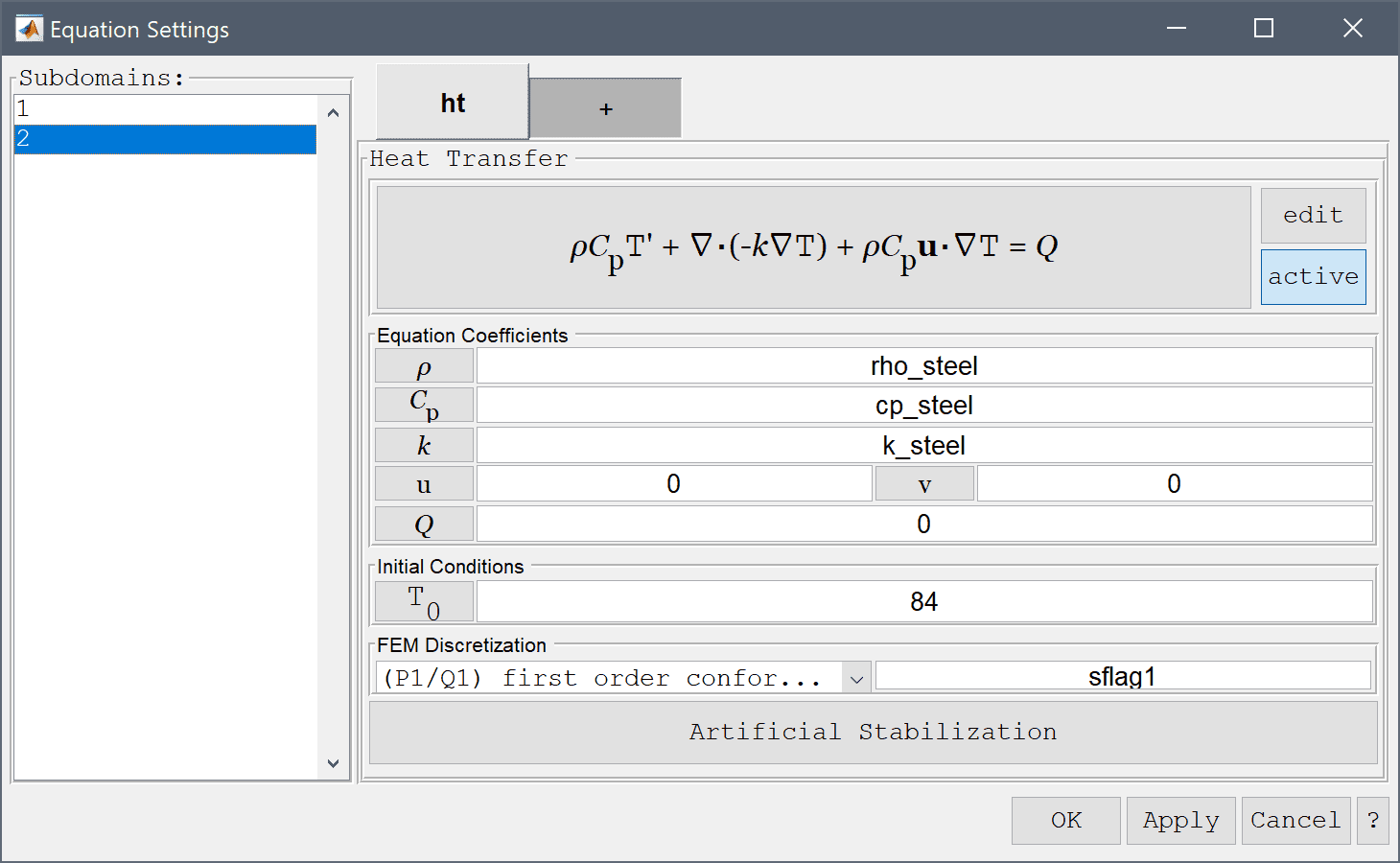
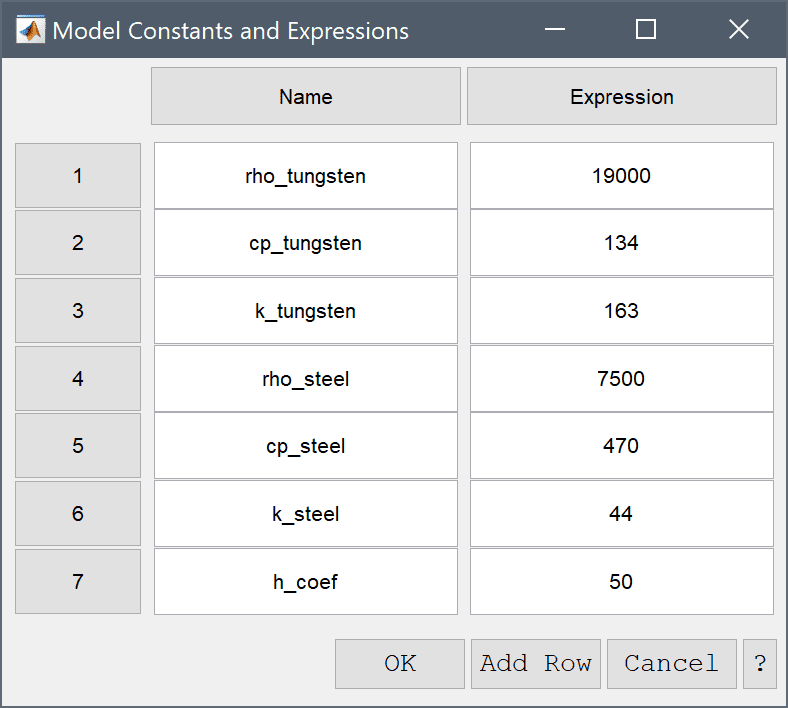
The Model Constants and Expressions functionality can be used to define and store convenient expressions, which then are available in the point, equation, boundary coefficients, and as postprocessing expressions. Here it is used to define the material parameters.
| Name | Expression |
|---|---|
| rho_tungsten | 19000 |
| cp_tungsten | 134 |
| k_tungsten | 163 |
| rho_steel | 7500 |
| cp_steel | 470 |
| k_steel | 44 |
| h_coef | 50 |
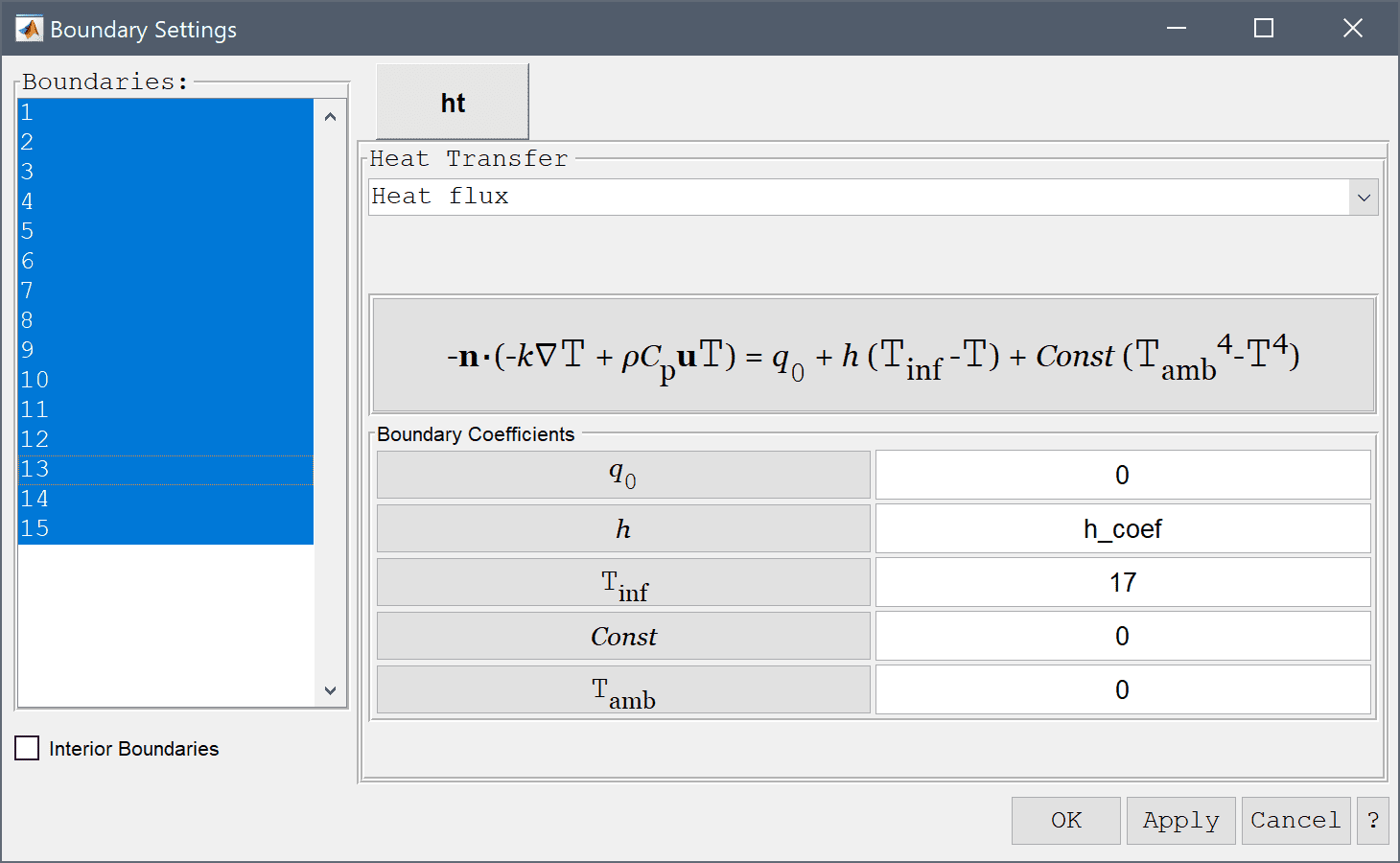
In the Boundary Settings dialog box, select the Heat flux boundary condition for all the boundaries. Enter h_coef in the edit field for the convective transfer coefficient h, and also enter 17 for the surrounding reference temperature Tinf.
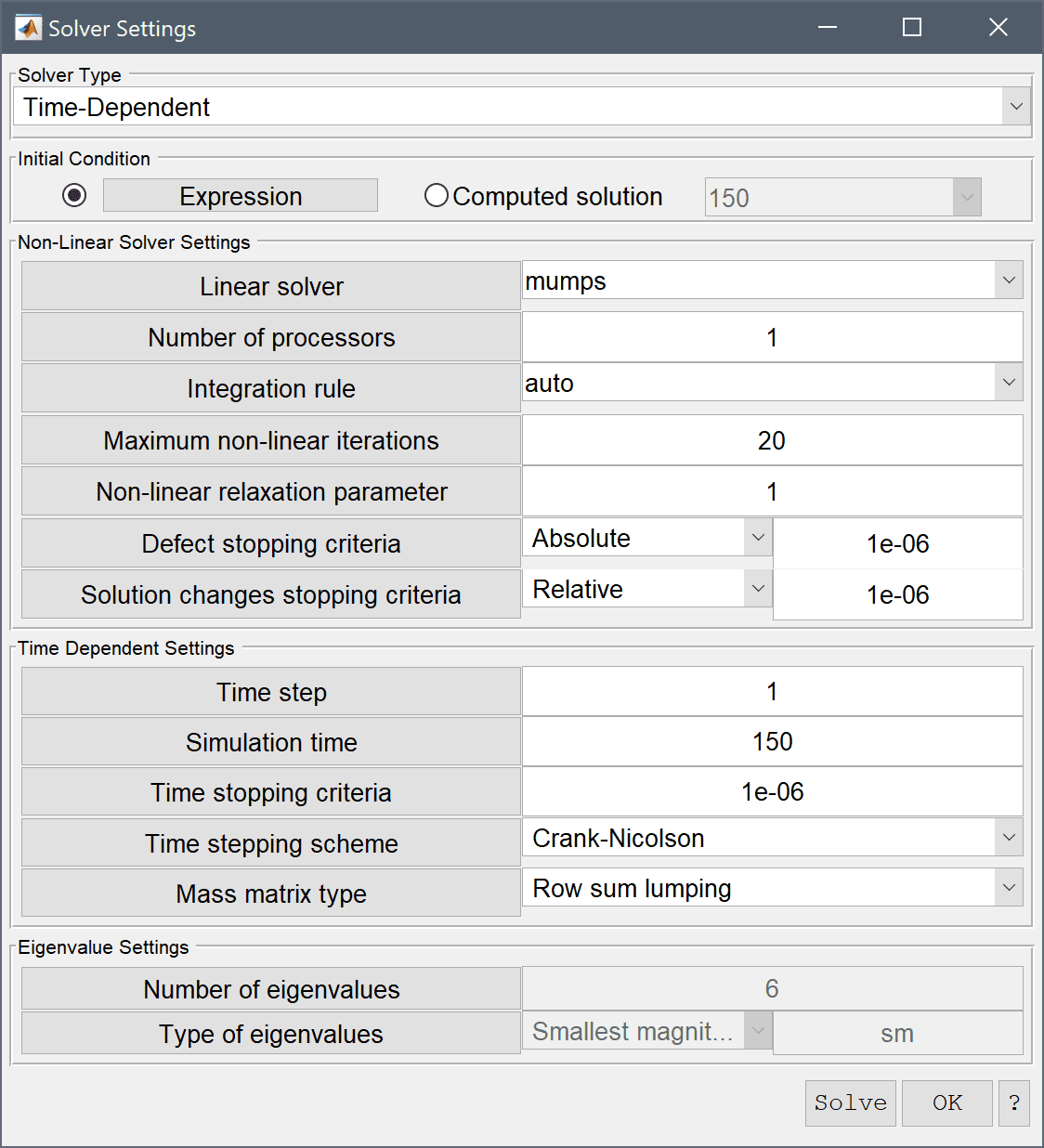
Now that the problem is fully specified, press the Solve mode button to switch to solve mode. Since this is a time dependent study, open the solver settings and select the Time-Dependent solver. Set the Time step to 1, Simulation time to 150, and then press Solve to start the solution process.
After the solver has finished, the toolbox will automatically switch to postprocessing mode, and show the resulting temperature field. Add some contour levels to more clearly see the different temperature levels.
Enter 20 into the Number or specified vector of contour levels to plot edit field.
Press Apply to plot and visualize the selected postprocessing options.
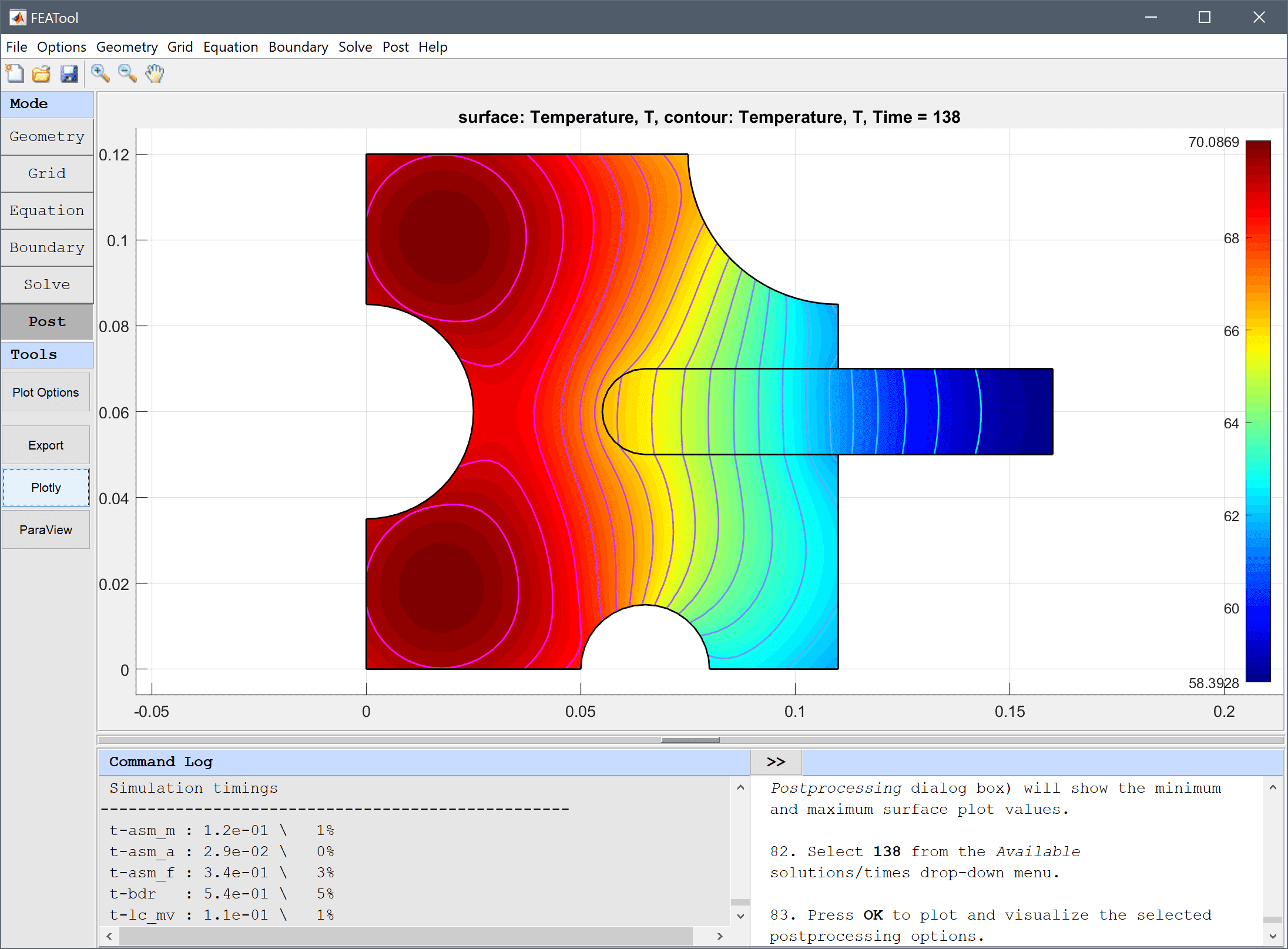
Plot solutions at different times and verify that the assembly has cooled to a temperature of 70 degrees around the time t = 138 s. Note that both the colorbar and limits field (in the Postprocessing dialog box) will show the minimum and maximum surface plot values.
More advanced processing can also be done by exporting the simulation data to the command line interface, where it can be accessed, modified, and used in scripts. (See for example the section on CLI postprocessing below.)
The shrink fitting of an assembly heat transfer model has now been completed and can be saved as a binary (.fea) model file, or exported as a programmable MATLAB m-script text file (available as the example ex_heattransfer5 script file), or GUI script (.fes) file.
More advanced postprocessing can be done on the MATLAB command line interface (CLI) console. To export the model data to the MATLAB CLI, select Export Model Data Struct to MATLAB option from the File menu. The model data will now be available as a variable named fea. The following script commands will find the time and plot the solution when the maximum temperature has reached 70 degrees.
% Find minimum, maxium, and time when max temperature = 70.
for i=1:length(tlist)
T_min(i) = min(fea.sol.u(:,i));
T_max(i) = max(fea.sol.u(:,i));
end
ind = find(T_max<70);
i1 = ind(1);
i2 = i1 - 1;
s = ( T_max(i2) - 70 )/( T_max(i2) - T_max(i1) );
t_70 = tlist(i2) + s*( tlist(i1) - tlist(i2) );
u_70 = fea.sol.u(:,i2) + s*( fea.sol.u(:,i1) - fea.sol.u(:,i2) );
% Plot temperature field at t_70.
fig = figure;
fea_plot = fea;
fea_plot.sol.u = u_70;
postplot( fea_plot, 'surfexpr', 'T', 'isoexpr', 'T', 'isolev', 20, 'parent', subplot(1,2,1) )
title(['Temperature distribution at t = ',num2str(t_70)])
% Plot min/max temperature curves as a function of time.
subplot(1,2,2)
plot( tlist, T_min, 'b-' )
hold on
plot( tlist, T_max, 'r-' )
grid on
title('Maximum and minimum temperatures')
ylabel('Temperature [C]')
xlabel('Time [s]')