A selection of tutorial models and examples are presented in this section. These and other model examples can also be selected and automatically run from the File > Model Examples and Tutorials... menu.

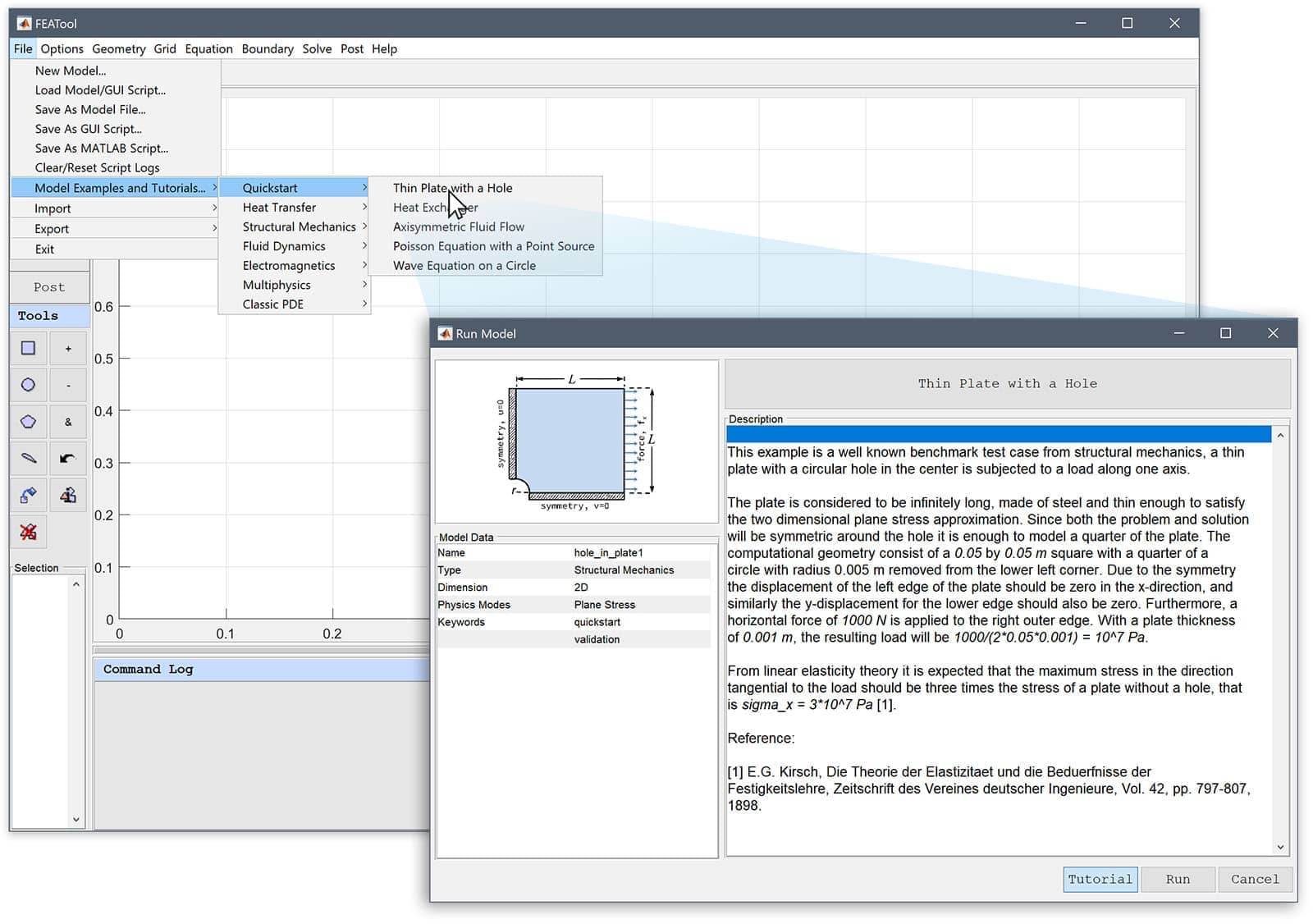
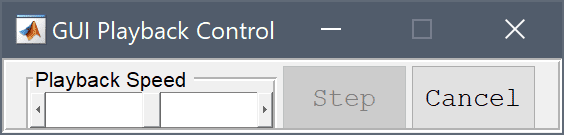
When an automated tutorial is selected, the Run Model dialog box will open and show a description and information about the tutorial example. The tutorial can be started by pressing the Run button. de-selecting the Tutorial mode toggle button will run the tutorial in fast automatic mode without any pauses. When a tutorial or finite element script (fes) model is run, the GUI Playback Control panel below is opened where the Playback Speed can be controlled via the slider. Setting the slider to the slowest (far left) setting pauses the tutorial playback and enables the Step button to manually step through the tutorial at ones own pace. Closing the playback control panel or pressing the Cancel button stops the tutorial at the current state.

Field	Description
ex_axistressstrain1	Axisymmetric stress-strain of a hollow cylinder.
ex_axistressstrain2	Axisymmetric stress-strain of a hollow sphere.
ex_axistressstrain3	Axisymmetric disc with fixed edge and point load.
ex_axistressstrain4	Stress formed in brake disk due to heat build up.
ex_axistressstrain5	Axisymmetric vibration modes of a hollow cylinder.
ex_brinkman1	Coupled porous and incompressible laminar flow.
ex_classicpde1	Eigenmodes for a circular drum.
ex_classicpde2	Eigenmodes for a L-shaped membrane.
ex_compressibleeuler1	1D compressible Euler SOD shock tube problem.
ex_compressibleeuler2	2D compressible Euler oblique shock problem.
ex_compressibleeuler3	2D compressible Euler reflected shock problem.
ex_compressibleeuler4	2D compressible Euler inviscid supersonic flow over a bump.
ex_compressibleeuler5	3D compressible Euler inviscid supersonic flow over a bump.
ex_compressibleeuler6	2D supersonic flow past a wedge with an oblique shock wave.
ex_convdiff1	Convection and diffusion on a unit square.
ex_convdiff2	Periodic convection and diffusion on a line with exact solution.
ex_convdiff3	Infinite time dependent convection and diffusion on a line.
ex_convdiff4	One dimensional Burgers equation with steady solution.
ex_convdiff5	Dominating convection example requiring artificial stabilization.
ex_convdiff6	1D stationary convection-diffusion-reaction with exact solution.
ex_convreact1	Time dependent one dimensional convection and reaction model.
ex_custom_equation1	Black-Scholes model equation implemented as a custom equation.
ex_darcy1	Porous media flow in a packed bed reactor using Darcy's law.
ex_diffusion1	Diffusion equation on a unit square with different solutions.
ex_diffusion2	Diffusion equation on a line with exact solutions.
ex_eddycurrents1	2D Eddy currents test problem solved vector (Nedelec) elements.
ex_eddycurrents2	3D Eddy currents test problem solved vector (Nedelec) elements.
ex_electrostatics1	Electrostatics test problem.
ex_electrostatics2	Axisymmetric model of a spherical capacitor.
ex_euler_beam1	1D Euler-Bernoulli beam example.
ex_euler_beam2	1D Euler-Bernoulli beam vibration mode example.
ex_euler_beam3	1D Euler-Bernoulli beam vibration example.
ex_fluidstructure1	Fluid-structure interaction for static flow past an elastic beam
ex_fluidstructure2	Fluid-solid interaction, instationary flow past an elastic beam
ex_fluidstructure3	2D Fluid-structure interaction for flow past an elastic beam
ex_fluidstructure4	3D Fluid-structure interaction for flow past an elastic beam
ex_heat_exchanger1	Free and forced convection in a heat exchanger.
ex_heat_exchanger2	Multi-Simulation heat exchanger.
ex_heattransfer1	2D heat conduction with natural convection and radiation.
ex_heattransfer2	One dimensional stationary heat transfer with radiation.
ex_heattransfer3	One dimensional transient heat conduction.
ex_heattransfer4	Two dimensional heat transfer with convective cooling.
ex_heattransfer5	Two dimensional transient cooling shrink fitting example.
ex_heattransfer6	Axisymmetric steady state heat conduction of a cylinder.
ex_heattransfer7	One dimensional transient heat conduction with analytic solution.
ex_heattransfer8	2D space-time formulation of one dimensional transient heat diffusion.
ex_heattransfer9	One dimensional transient heat conduction with point source.
ex_heattransfer10	Conjugate heat transfer test example with multiple domains.
ex_laplace1	Laplace equation on a unit square.
ex_laplace2	Laplace equation on a unit circle.
ex_linearelasticity1	Linear elasticity test case, solid stress-strain for a cube.
ex_linearelasticity2	Three dimensional example of stress on a bracket.
ex_linearelasticity3	Parametric study of the bracket deformation model.
ex_linearelasticity4	Stress of loaded I-beam supported by two brackets.
ex_linearelasticity5	Vibration of a square plate.
ex_linearelasticity6	NAFEMS benchmark LE6, skew plate under normal pressure.
ex_magnetostatics1	Magnetostatics test problem.
ex_magnetostatics2	Magnet field around a horseshoe magnet.
ex_magnetostatics3	Cylindrical magnet without electrical currents.
ex_magnetostatics4	Axisymmetric model of cylindrical magnet.
ex_magnetostatics5	2D Magnetostatics test model.
ex_multiphase1	Multiphase flow example of a static bubble.
ex_multiphase2	Multiphase flow example of a rising bubble.
ex_multiphase3	Multiphase flow example of a breaking dam.
ex_natural_convection	Natural convection in a square cavity.
ex_navierstokes1	Incompressible fluid flow in a channel.
ex_navierstokes2	Incompressible driven cavity flow.
ex_navierstokes3	Incompressible fluid flow around a cylinder in a channel (Re=20).
ex_navierstokes3b	Flow around a cylinder solver benchmark.
ex_navierstokes4	Incompressible fluid flow over a backwards facing step.
ex_navierstokes5	Two dimensional decay of a standing vortex.
ex_navierstokes6	Time dependent flow around a cylinder in a channel (0<=Re<=100).
ex_navierstokes7	Laminar flow in a curved three dimensional pipe.
ex_navierstokes8	Axisymmetric flow in a in constricted circular pipe.
ex_navierstokes8b	Axisymmetric pipe flow solver benchmark.
ex_navierstokes9	Axisymmetric impinging jet.
ex_navierstokes10	3D flow in a pipe using the OpenFOAM solver.
ex_navierstokes11	3D cavity flow in a cube using the OpenFOAM solver.
ex_navierstokes12	3D flow over a backwards facing step using the OpenFOAM solver.
ex_navierstokes13	3D flow past a cylinder using the OpenFOAM solver.
ex_navierstokes14	Axisymmetric flow in a pipe due to pressure difference.
ex_navierstokes15	2D channel flow due to periodic pressure gradient.
ex_navierstokes16	2D flow past a cylinder with an attached fixed beam.
ex_navierstokes17	Turbulent 2D flow in a channel.
ex_nonnewtonian1	2D non-Newtonian power-law flow in a channel.
ex_nonlinear_pde1	1D nonlinear PDE with analytical solution.
ex_nonlinear_pde2	1D nonlinear PDE with analytical solution extended to 2D.
ex_periodic1	Moving 1D pulse in a periodic domain.
ex_periodic2	2D Periodic Poisson equation example.
ex_piezoelectric1	Bending of a beam due to piezoelectric effects.
ex_planestrain1	2D Plane strain analysis of a pressure vessel.
ex_planestrain2	Plane strain analysis of a pressure vessel.
ex_planestress1	Stress computation for a hole in a thin plate.
ex_planestress2	NAFEMS plane stress benchmark example.
ex_planestress3	NAFEMS benchmarks IC1-4, plane stress analysis of a tapered plate.
ex_planestress4	NAFEMS benchmark T1, plate deformation due to thermal stress.
ex_planestress5	NAFEMS benchmark LE1, plane stress in an elliptic membrane.
ex_planestress6	2D Plane stress analysis of a pressure vessel.
ex_planestress7	Thermally induced displacements on a rectangle.
ex_poisson1	Poisson equation on a line.
ex_poisson2	Poisson equation on a circle.
ex_poisson3	Poisson equation on a unit square.
ex_poisson4	Poisson equation on a rectangle with complex solution.
ex_poisson5	Poisson equation on a sphere.
ex_poisson6	Poisson equation on a unit cube.
ex_poisson7	Poisson equation on a unit circle with a point constraint.
ex_poisson8	Poisson equation on a unit square with all Neumann boundary conditions and integral constraint.
ex_potential_flow1	Potential flow around a NACA wing profile.
ex_resistive_heating1	Resistive heating of a spiral tungsten filament.
ex_resistive_heating2	Nonlinear resistive heating in a conducting plate.
ex_robinbc1	1D example with a Robin boundary condition.
ex_spanner	Gmsh import of a mesh and stress calculation in a spanner.
ex_swirl_flow1	2D axisymmetric swirl flow in a tube with analytic solution.
ex_swirl_flow2	2D axisymmetric swirl flow in a stepped narrowing tubular region.
ex_swirl_flow3	2D axisymmetric time dependent Taylor-Couette swirl flow.
ex_swirl_flow4	2D axisymmetric swirl flow around a rotating disk.
ex_waveequation1	Wave equation on a unit circle.
ex_schrodinger1	The Schrödinger equation for a Hydrogen atom.

Heat Transfer

Fluid Dynamics

Structural Mechanics

Electromagnetics

Multiphysics

Classic PDE

Script File Examples